Предмет: Геометрия,
автор: OksankaВL
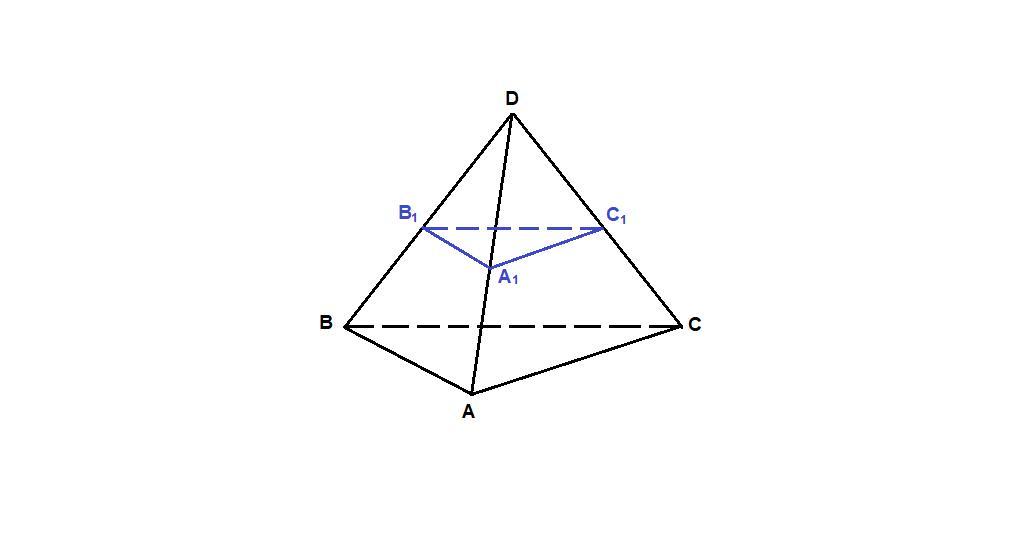
В тетраэдре DABC точки А1, В1 и С1 середины рёбер DA, DB и DC соответственно. Докажите подобие треугольников АВС и А1В1С1 Найдите площадь треугольника А1В1С1 если площадь треугольника АВС равна 44см2
Ответы
Автор ответа:
0
Ответ:
11 см²
Объяснение:
Точки А₁, В₁ и С₁ середины ребер тетраэдра, значит
А₁В₁ - средняя линия ΔDAB и А₁В₁ = 1/2 АВ,
А₁С₁ - средняя линия ΔDAС и А₁С₁ = 1/2 АС,
В₁С₁ - средняя линия ΔDВС и В₁С₁ = 1/2 ВС,
Т.е. стороны треугольника А₁В₁С₁ пропорциональны сторонам треугольника АВС, значит
ΔА₁В₁С₁ подобен ΔАВС по трем пропорциональным сторонам.
Коэффициент подобия:
k = A₁B₁ / AB = 1/2
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sa₁b₁c₁ / Sabc = k² = 1/4
Sa₁b₁c₁ = Sabc / 4 = 44 / 4 = 11 см²
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: animeshnikya61
Предмет: Математика,
автор: damirgggg7777
Предмет: Математика,
автор: anelomarova61
Предмет: Математика,
автор: Maka4ron
Предмет: Литература,
автор: vovan85323