Предмет: Алгебра,
автор: rrrrtttt01
Пожалуйста помогите.........................
Приложения:
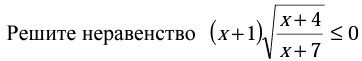

Ответы
Автор ответа:
0
1.

ОДЗ
х+7≠0
х≠-7

Поскольку корень не может принимать отрицательные значения, то
х+1≤0
х≤-1
х∈(-∞; -1)
Объединим с ОДЗ
х∈(-∞; -7)∨[-4; -1]
Ответ х∈(-∞; -7)∨[-4; -1]
2.
f(x)=ax²-6x+3
Здесь следует рассмотреть данную функцию как график.
Это парабола.Следовательно наименьшее и наибольшее значение может быть в вершине параболы. Рассмотрим 2 варианта
а) a<0
f(x)=ax²-6x+3 - ветви направлены вниз, точки минимума нет, т.к. график стремится к -∞. Будет существовать только точка максимума. Она же вершина параболы.
б) а>0
f(x)=ax²-6x+3 - ветви направлены вверх, точка минимума вершина параболы
x₀=-b/2a=-(-6)/(2a)=3/a
По условию значение в этой точке меньше 2,5, а значит
f(3/a)=a*(3/a)²-6*3/a+3=9/a-18/a+3=-9/a+3<2.5
-9/a+3<2.5
9/a-0.5>0
(18-a)/2a>0
(a-18)/a<0
a∈(0; 18]
Ответ a∈(0; 18]
ОДЗ
х+7≠0
х≠-7
Поскольку корень не может принимать отрицательные значения, то
х+1≤0
х≤-1
х∈(-∞; -1)
Объединим с ОДЗ
х∈(-∞; -7)∨[-4; -1]
Ответ х∈(-∞; -7)∨[-4; -1]
2.
f(x)=ax²-6x+3
Здесь следует рассмотреть данную функцию как график.
Это парабола.Следовательно наименьшее и наибольшее значение может быть в вершине параболы. Рассмотрим 2 варианта
а) a<0
f(x)=ax²-6x+3 - ветви направлены вниз, точки минимума нет, т.к. график стремится к -∞. Будет существовать только точка максимума. Она же вершина параболы.
б) а>0
f(x)=ax²-6x+3 - ветви направлены вверх, точка минимума вершина параболы
x₀=-b/2a=-(-6)/(2a)=3/a
По условию значение в этой точке меньше 2,5, а значит
f(3/a)=a*(3/a)²-6*3/a+3=9/a-18/a+3=-9/a+3<2.5
-9/a+3<2.5
9/a-0.5>0
(18-a)/2a>0
(a-18)/a<0
a∈(0; 18]
Ответ a∈(0; 18]
Похожие вопросы
Предмет: Английский язык,
автор: lizapogodinacom
Предмет: Английский язык,
автор: Xalivza
Предмет: Геометрия,
автор: GolovachLenaOriginal
Предмет: Алгебра,
автор: Inna56