Question

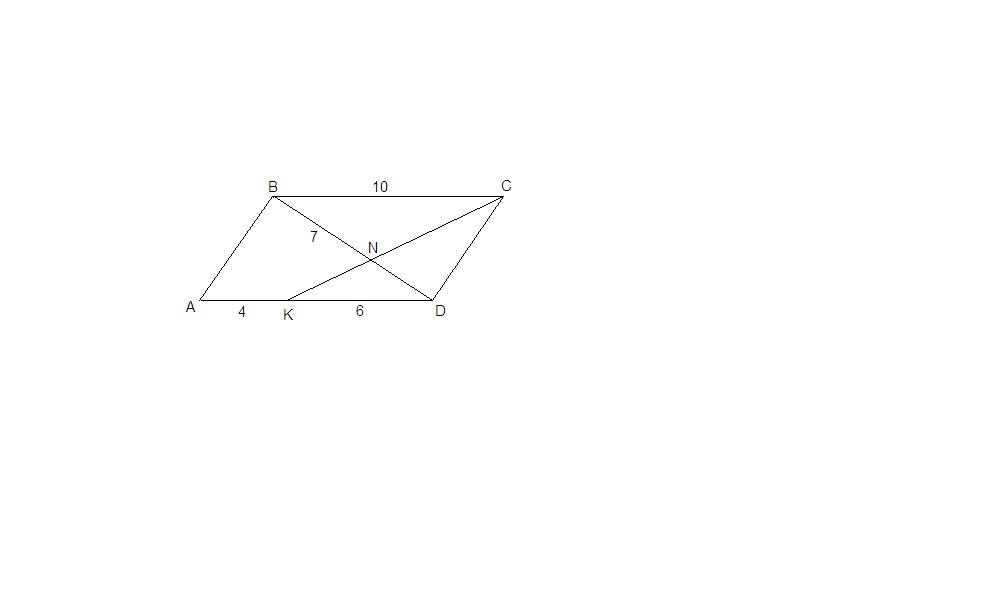
в параллелограмме АВСД точка К лежит на стороне АД отрезок СК пересекает диагональ ВД в точке N А)докажите что треугольники BNC и DNK подобны б) найдите длину диагонали ВД если известно что ВС=10 АК=4 BN=7

Answer 1

∠СВN = ∠KDN как накрест лежащие при пересечении параллельных прямых AD и ВС секущей BD,
∠CNB = ∠KND как вертикальные, значит
ΔBNC подобен ΔDNK по двум углам.
Тогда
BN : ND = BC : KD
KD = AD - AK = 10 - 4 = 6 (AD = BC = 10 как противолежащие стороны параллелограмма)
7 : ND = 10 : 6
ND = 6 · 7 / 10 = 42/10 = 4,2
BD = BN + ND = 7 + 4,2 = 11,2