Предмет: Алгебра,
автор: Лена2607
ЛОГАРИФМЫ. Решите, пожалуйста
Приложения:
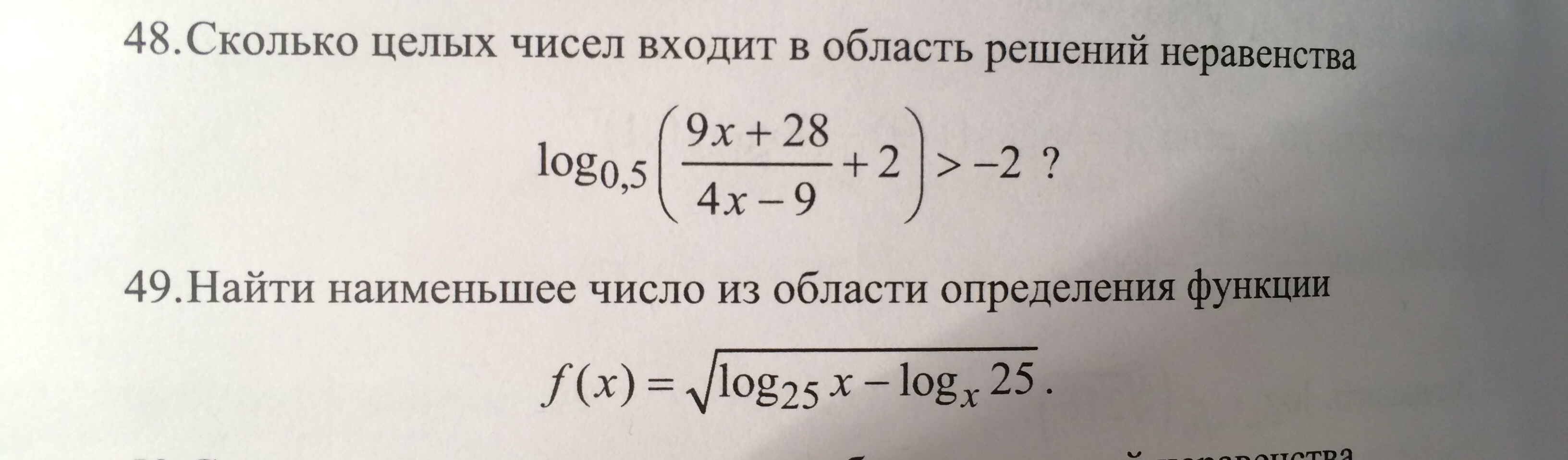
Ответы
Автор ответа:
0
1.Запишем ОДЗ.








Пересекаем с ОДЗ, имеем 2 числовые прямые.

x∈(-46;-10/17) => целых чисел 45, так ккак -46 не входит в область решений, выколотая точка мы считает от неё.
2.



Перекрещиваем с областью определения, выкалываем точку х = 1 и получаем след.интервалы х∈( ∪(25;
∪(25; ) или 1/25 < x < 1 и x>25. Таким образом, наименьшее число в области определения
) или 1/25 < x < 1 и x>25. Таким образом, наименьшее число в области определения 
Пересекаем с ОДЗ, имеем 2 числовые прямые.
x∈(-46;-10/17) => целых чисел 45, так ккак -46 не входит в область решений, выколотая точка мы считает от неё.
2.
Перекрещиваем с областью определения, выкалываем точку х = 1 и получаем след.интервалы х∈(
Похожие вопросы
Предмет: Українська мова,
автор: Sasha57273
Предмет: Українська мова,
автор: wolfgangshoot
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Юляша111222