Предмет: Математика,
автор: 89080657780
Помогите пожалуйста решить
Приложения:
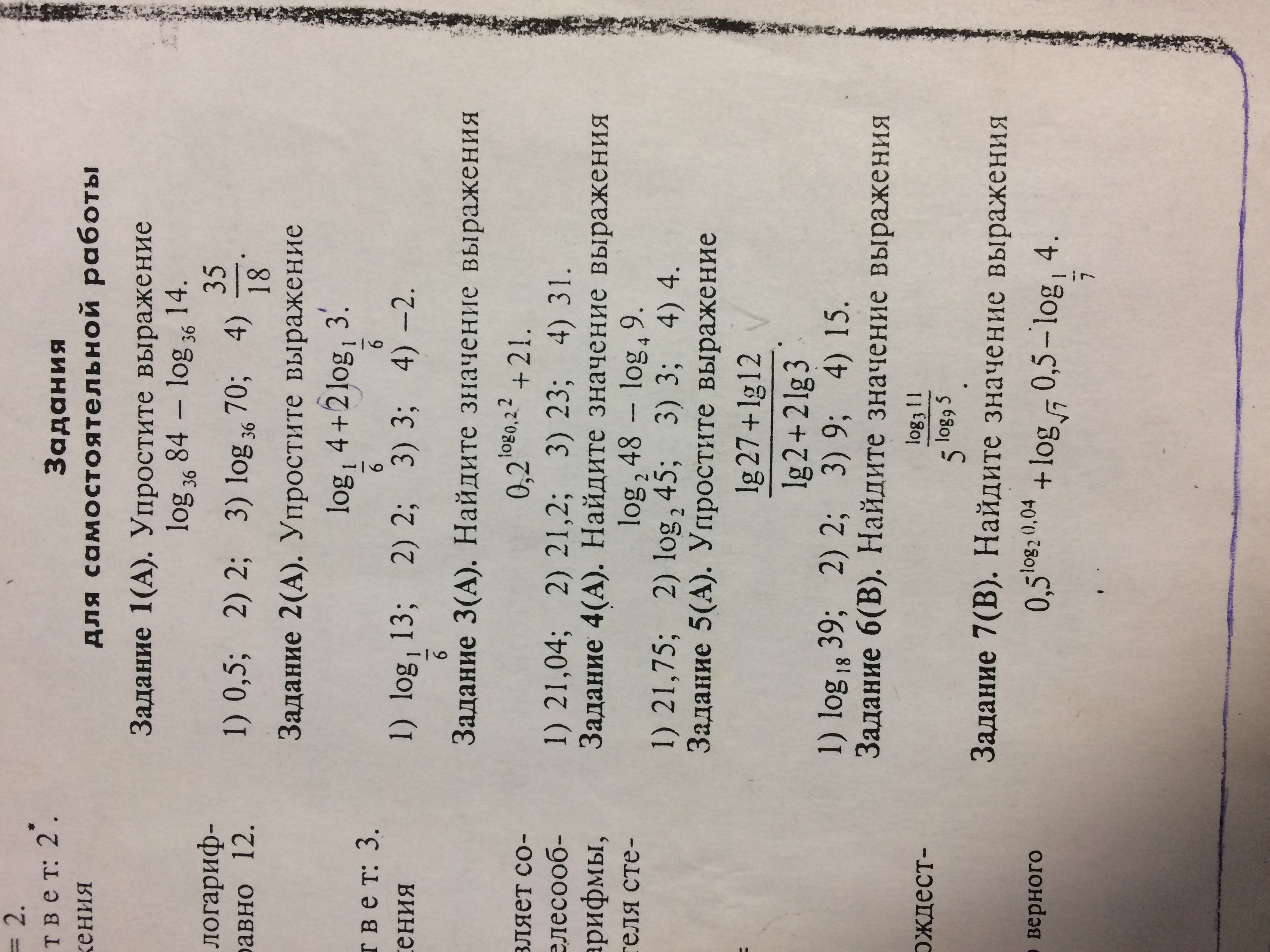
Ответы
Автор ответа:
0
Приложения:
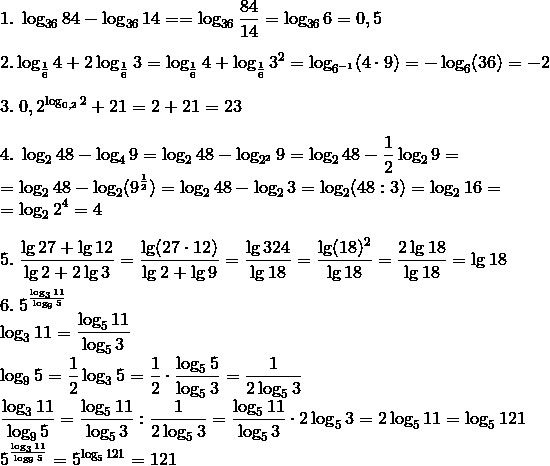
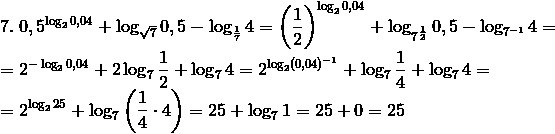
Похожие вопросы
Предмет: Русский язык,
автор: kuznecove557
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: FanikNazanik666
Предмет: Математика,
автор: Аноним