Предмет: Алгебра,
автор: Хомячоок
помогите пожалуйста алгебра 11 класс логарифмы
Приложения:
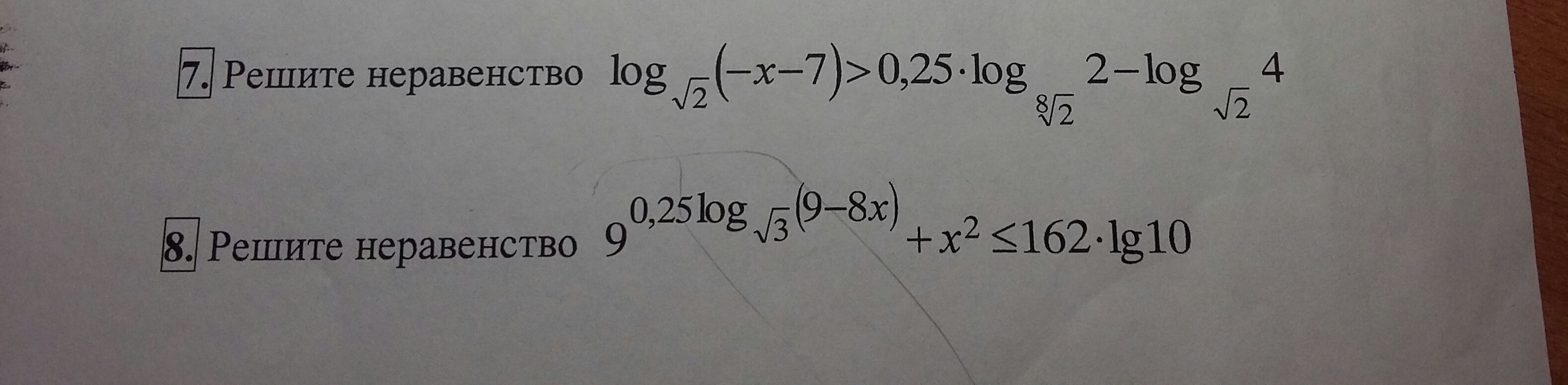
Ответы
Автор ответа:
0
Первое неравенство: ![log_{sqrt{2}}(-x-7) textgreater 0,25*log_{sqrt[8]{2}}2-log_{sqrt{2}}4 log_{sqrt{2}}(-x-7) textgreater 0,25*log_{sqrt[8]{2}}2-log_{sqrt{2}}4](https://tex.z-dn.net/?f=log_%7Bsqrt%7B2%7D%7D%28-x-7%29+textgreater++0%2C25%2Alog_%7Bsqrt%5B8%5D%7B2%7D%7D2-log_%7Bsqrt%7B2%7D%7D4)
ОДЗ:
![0,25*log_{sqrt[8]{2}}2-log_{sqrt{2}}4=0,25*log_{2^{frac{1}{8}}}2-log_{2^{frac{1}{2}}}4=\0,25*8log_22-2log_24=-2 0,25*log_{sqrt[8]{2}}2-log_{sqrt{2}}4=0,25*log_{2^{frac{1}{8}}}2-log_{2^{frac{1}{2}}}4=\0,25*8log_22-2log_24=-2](https://tex.z-dn.net/?f=0%2C25%2Alog_%7Bsqrt%5B8%5D%7B2%7D%7D2-log_%7Bsqrt%7B2%7D%7D4%3D0%2C25%2Alog_%7B2%5E%7Bfrac%7B1%7D%7B8%7D%7D%7D2-log_%7B2%5E%7Bfrac%7B1%7D%7B2%7D%7D%7D4%3D%5C0%2C25%2A8log_22-2log_24%3D-2)
теперь левая часть:
 всё тоже, что и
всё тоже, что и 

Ответ: x∈(–∞; –7)
Второе неравенство:
ОДЗ:
для начала проясним, что , следовательно правая часть неравенства просто равна 162; продолжаем решать, преобразовывая первое слагаемое, в показатели степени которого стоит логарифм:
, следовательно правая часть неравенства просто равна 162; продолжаем решать, преобразовывая первое слагаемое, в показатели степени которого стоит логарифм:

от логарифма в степени мы перешли к классной разности девятки и восьми иксов, только что разве украшающей наше неравенство, ну а мы продолжаем: всё тоже, что и
всё тоже, что и  — изичное квадратное неравенство, решаем и его:
— изичное квадратное неравенство, решаем и его:

Ответ (решение неравенства, не включая ОДЗ): x∈[–9; 17]
Переплетя с ОДЗ, мы получим ответ: x∈[–9; 1,125)
ОДЗ:
теперь левая часть:
Ответ: x∈(–∞; –7)
Второе неравенство:
ОДЗ:
для начала проясним, что
от логарифма в степени мы перешли к классной разности девятки и восьми иксов, только что разве украшающей наше неравенство, ну а мы продолжаем:
Ответ (решение неравенства, не включая ОДЗ): x∈[–9; 17]
Переплетя с ОДЗ, мы получим ответ: x∈[–9; 1,125)
Автор ответа:
0
СПАСИБО ОГРОМНОЕ!
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: История,
автор: alenazaharcenko359
Предмет: Литература,
автор: Dmitrygurov6446
Предмет: Математика,
автор: kateushakowa