Предмет: Алгебра,
автор: 55Mari55
Помогите решить уравнения))) Срочно.
Приложения:
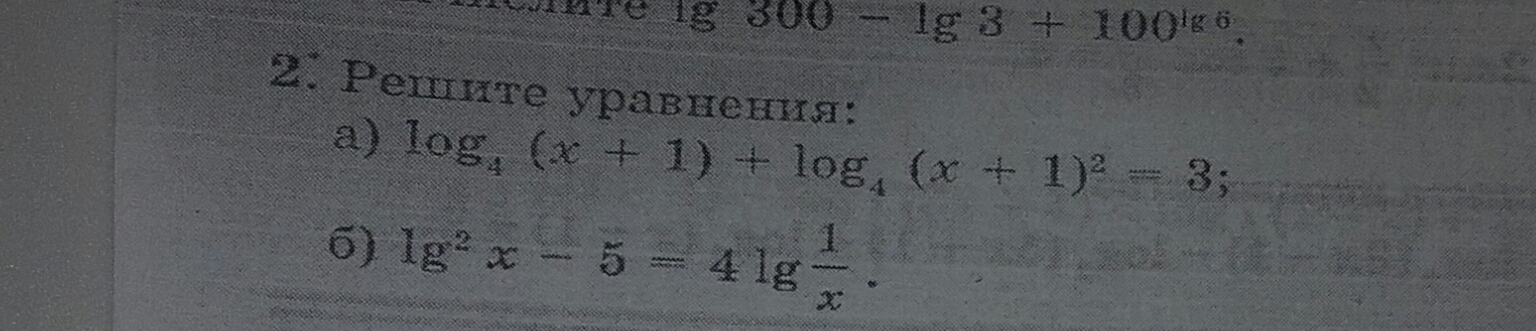
Ответы
Автор ответа:
0
а) ОДЗ: x+1>0, <=> x>-1.
Исходное уравнение равносильно следующему:




 .
.
Ответ. {3}.
б) ОДЗ: x>0.
Исходное уравнение равносильно следующему

сделаем замену lg(x)=t, тогда





t+5 = 0 или t-1=0,
t = -5 или t=1;
lg(x) = -5 или lg(x)=1;
x=10^(-5) = 1/100000 = 0,00001 или x=10^1 = 10.
Ответ. {0,00001; 10}.
Исходное уравнение равносильно следующему:
Ответ. {3}.
б) ОДЗ: x>0.
Исходное уравнение равносильно следующему
сделаем замену lg(x)=t, тогда
t+5 = 0 или t-1=0,
t = -5 или t=1;
lg(x) = -5 или lg(x)=1;
x=10^(-5) = 1/100000 = 0,00001 или x=10^1 = 10.
Ответ. {0,00001; 10}.
Похожие вопросы
Предмет: Українська мова,
автор: stand2magaz
Предмет: Другие предметы,
автор: alexivahnukss
Предмет: Математика,
автор: markwahlberg
Предмет: Математика,
автор: LUNTIK1212