Question

РЕШИТЕ ПОЖАЛУЙСТА!!! ДАЮ 99 БАЛЛОВ
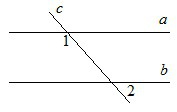
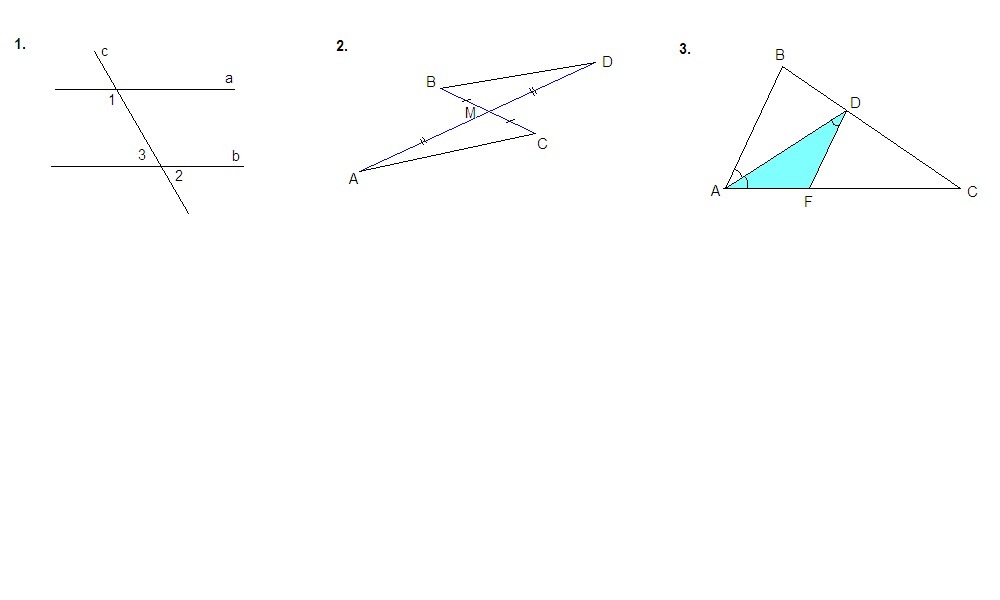
1.На рисунке прямые a и b параллельны, .угол 1 = 115°. Найдите угол 2.(РИСУНОК СНИЗУ К ПЕРВОМУ ЗАДАНИЮ)
2.Отрезки АD и BC пересекаются в их общей середине точке М. Докажите, что прямые АС и ВD параллельны.
3.Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне AB и пересекающая сторону AC в точке F. Найдите углы треугольника ADF, если hello_html_m3b8c471b.gifBAC =72°.

Answer 1

1. ∠1 + ∠3 = 180° так как эти углы внутренние односторонние при пересечении параллельных прямых а и b секущей с.

∠3 = 180° - ∠1 = 180° - 115° = 65°

∠2 = ∠3 = 65° так как эти углы вертикальные.

2. AM = MD, BM = MC так как по условию М - середина отрезков AD и ВС,

∠АМС = ∠DMB как вертикальные, ⇒ ΔАМС = ΔDMB по двум сторонам и углу между ними.

Значит ∠МАС = ∠MDB, а эти углы накрест лежащие при пересечении прямых АС и BD секущей AD, ⇒ АС ║ BD.

3. ∠DAF = ∠DAB = 1/2 ∠BAC = 1/2 · 72° = 36°, так как AD биссектриса.

∠FDA =∠DAB = 36° как накрест лежащие при пересечении АВ║DF секущей AD,

∠AFD = 180° - (∠DAF + ∠FDA) = 180° - (36° + 36°) = 180° - 72° = 108°