Предмет: Математика,
автор: Chappi19
Помогите решить!
Неравенства показательные.
3 ^(-x + 13) > 729.......................... (-х+13)-Степень
2^x + 2^(x + 2) > 640....................(x+2)-Степень
4^x + 4^(x + 2) < 272
Приложения:
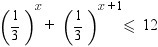
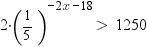
Ответы
Автор ответа:
0
3^ (-x+13) >729
3^(-x + 13) > 3^6
-x+13>6
13-6>x
x<7
x∈(-∞;7)
2^x +2^(x+2) >640
2^x + 2^x × 2^2 > 640
2^x × (1 + 2^2) > 640
2^x × 5 >640
2^x > 640/5
2^x > 128
2^x > 2^7
x>7
x∈ (7; +∞)
4^x +4^(x+2) <272
4^x + 4^x × 4^2 <272
4^x × ( 1+ 4^2) < 272
4^x × 17 < 272
4^x < 272/17
4^x < 16
4^x < 4^2
x<2
x∈ (-∞ ; 2 )
(1/3)^x + (1/3) ^(x+1) ≤ 12
(1/3)^x × (1 + 1/3 ) ≤ 12
1/3 ^x ≤ 12 ÷ 1 1/3
1/3 ^x ≤ 12/1 * 3/4
3^(-x) ≤ 9
3^ (-x) ≤ 3^2
-x≤ 2
x ≥ - 2
x∈ [ - 2 ; +∞)
2 × (1/5) ^ (-2x - 18) > 1250
5^ ( - 1*( -2x -18)) > 1250/2
5^ (2x +18) > 625
5^(2x+18) > 5^4
2x + 18 > 4
2x > 4 -18
x> -14/2
x > - 7
x (- 7 ; + ∞)
3^(-x + 13) > 3^6
-x+13>6
13-6>x
x<7
x∈(-∞;7)
2^x +2^(x+2) >640
2^x + 2^x × 2^2 > 640
2^x × (1 + 2^2) > 640
2^x × 5 >640
2^x > 640/5
2^x > 128
2^x > 2^7
x>7
x∈ (7; +∞)
4^x +4^(x+2) <272
4^x + 4^x × 4^2 <272
4^x × ( 1+ 4^2) < 272
4^x × 17 < 272
4^x < 272/17
4^x < 16
4^x < 4^2
x<2
x∈ (-∞ ; 2 )
(1/3)^x + (1/3) ^(x+1) ≤ 12
(1/3)^x × (1 + 1/3 ) ≤ 12
1/3 ^x ≤ 12 ÷ 1 1/3
1/3 ^x ≤ 12/1 * 3/4
3^(-x) ≤ 9
3^ (-x) ≤ 3^2
-x≤ 2
x ≥ - 2
x∈ [ - 2 ; +∞)
2 × (1/5) ^ (-2x - 18) > 1250
5^ ( - 1*( -2x -18)) > 1250/2
5^ (2x +18) > 625
5^(2x+18) > 5^4
2x + 18 > 4
2x > 4 -18
x> -14/2
x > - 7
x (- 7 ; + ∞)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: MinaYoo
Предмет: Литература,
автор: nurzankudysev1
Предмет: Геометрия,
автор: britvindima064
Предмет: Математика,
автор: Аноним