Предмет: Алгебра,
автор: gt60
Решите пожалуйста, только полностью распишите.
Приложения:
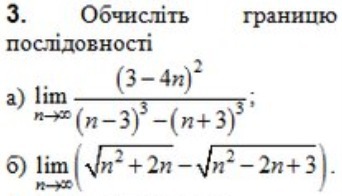
Ответы
Автор ответа:
0
В знаменателе разница кубов, раскладываем её.




Домножаем на сопряженное, чтобы получилась разность квадратов в числителе.




Домножаем на сопряженное, чтобы получилась разность квадратов в числителе.
Похожие вопросы
Предмет: Химия,
автор: bogdanaromanuk5
Предмет: Геометрия,
автор: plohanasti
Предмет: Физика,
автор: lr05
Предмет: Математика,
автор: EloviyKartofel
Предмет: Биология,
автор: Yoghurt