Предмет: Алгебра,
автор: rrrrtttt01
Решить систему.....................................
Приложения:
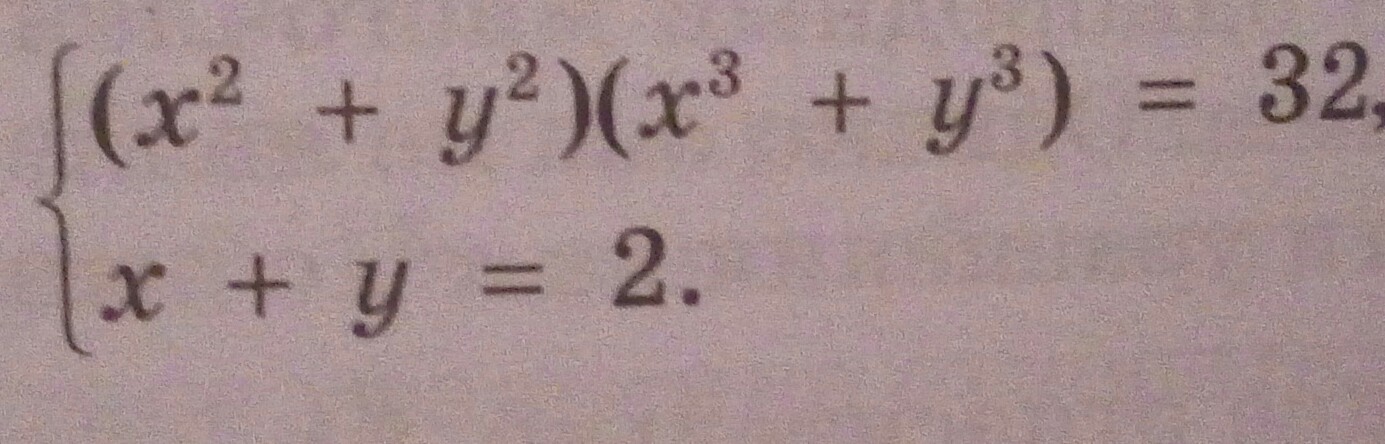
Ответы
Автор ответа:
0
В первом уравнении записано произведение, равное нулю.
Если х=0, то из второго уравнения у=2.
Если у=0, то из второго уравнения х=2.
Если x и y не равны 0, то первое уравнение можно упростить:
Последнее уравнение не имеет решений.
Ответ: (0; 2); (2; 0)
Похожие вопросы
Предмет: Музыка,
автор: 227384
Предмет: Биология,
автор: dianakiriliv
Предмет: Английский язык,
автор: Marishhka
Предмет: Математика,
автор: natali33339