Предмет: Алгебра,
автор: gl18
-корень из 2*sin(-5*пи/2+x)*sin(x) = cos(x) на промежутке [9пи/2;6пи]
корень из 2*sin(3*пи/2-x)*sin(x) = cos(x) на промежутке [-5пи;-4пи]
если не понятно что написанно есть фотография.
Приложения:
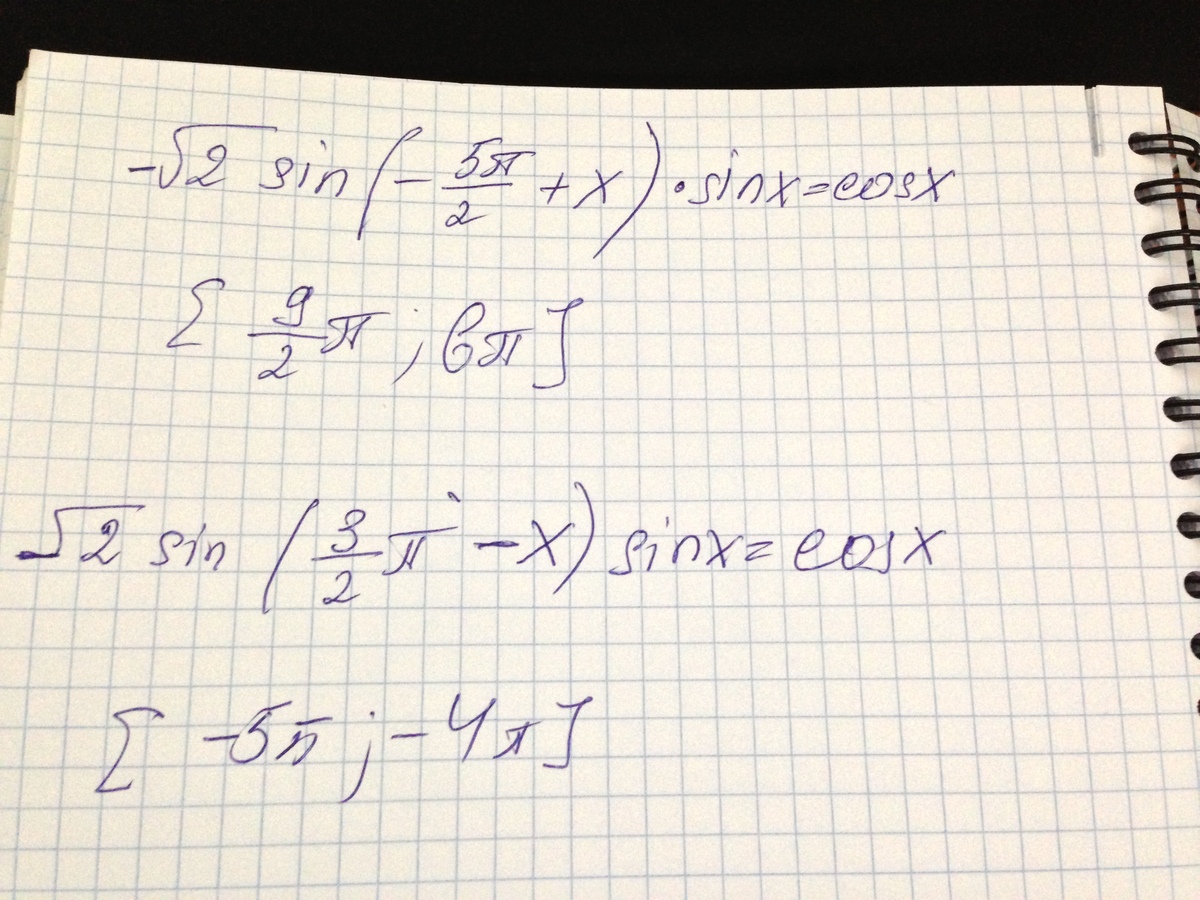
Ответы
Автор ответа:
0
1)
Корни считаем методот подбора.
В ответ записываем x которые я получил, если брать другие n и k значения х в промежуток входить небудут. И не забывай,там где надо писать что n принадлежит Z, k принадлежит Z. Значок принадлежит я ненашёл.
2)
Корни считаем методом подбора.
Похожие вопросы
Предмет: Геометрия,
автор: liyalove666
Предмет: Математика,
автор: Аноним
Предмет: Другие предметы,
автор: sebnemmsp
Предмет: Литература,
автор: Аноним