Предмет: Алгебра,
автор: kristinaivanenko
Помогите решить иррациональные неравенства
Приложения:
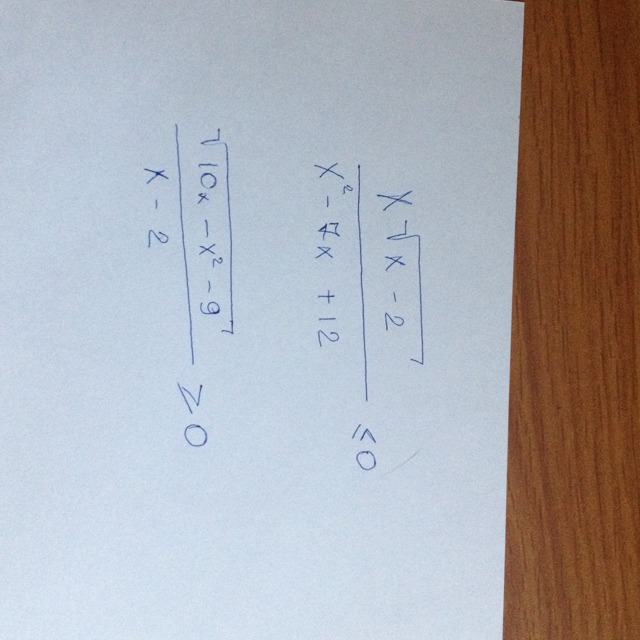
Ответы
Автор ответа:
0
Второе

Возведем обе части в квадрат

Нижняя часть не может быть равна нулю, её мы получили возведя в квадрат
x-2, значит
Верхняя часть может быть равной или больше нуля.
Решим квадратное уравнение

Верхняя часть равна нулю при x=1,9
Так как D>0, то она больше 0 при x∈(1;9)
Но если верхняя часть положительна, то x-2 тоже должна быть положительна.
Отсюда x-2>0, если верхняя часть не равна нулю.
Верхняя часть равна нулю при x=1.
Значит, неравенство выполняется при x∈(2;9], x=1.
Возведем обе части в квадрат
Нижняя часть не может быть равна нулю, её мы получили возведя в квадрат
x-2, значит
Верхняя часть может быть равной или больше нуля.
Решим квадратное уравнение
Верхняя часть равна нулю при x=1,9
Так как D>0, то она больше 0 при x∈(1;9)
Но если верхняя часть положительна, то x-2 тоже должна быть положительна.
Отсюда x-2>0, если верхняя часть не равна нулю.
Верхняя часть равна нулю при x=1.
Значит, неравенство выполняется при x∈(2;9], x=1.
Автор ответа:
0
Еще x-2>0, поэтому 9>=x>2
Похожие вопросы
Предмет: Қазақ тiлi,
автор: nandiobzory
Предмет: Математика,
автор: Diniaki
Предмет: История,
автор: kksaint
Предмет: Алгебра,
автор: nastya98kg
Предмет: Алгебра,
автор: NikaZ26