Предмет: Алгебра,
автор: miiron
Помогите решить 140,141
Приложения:
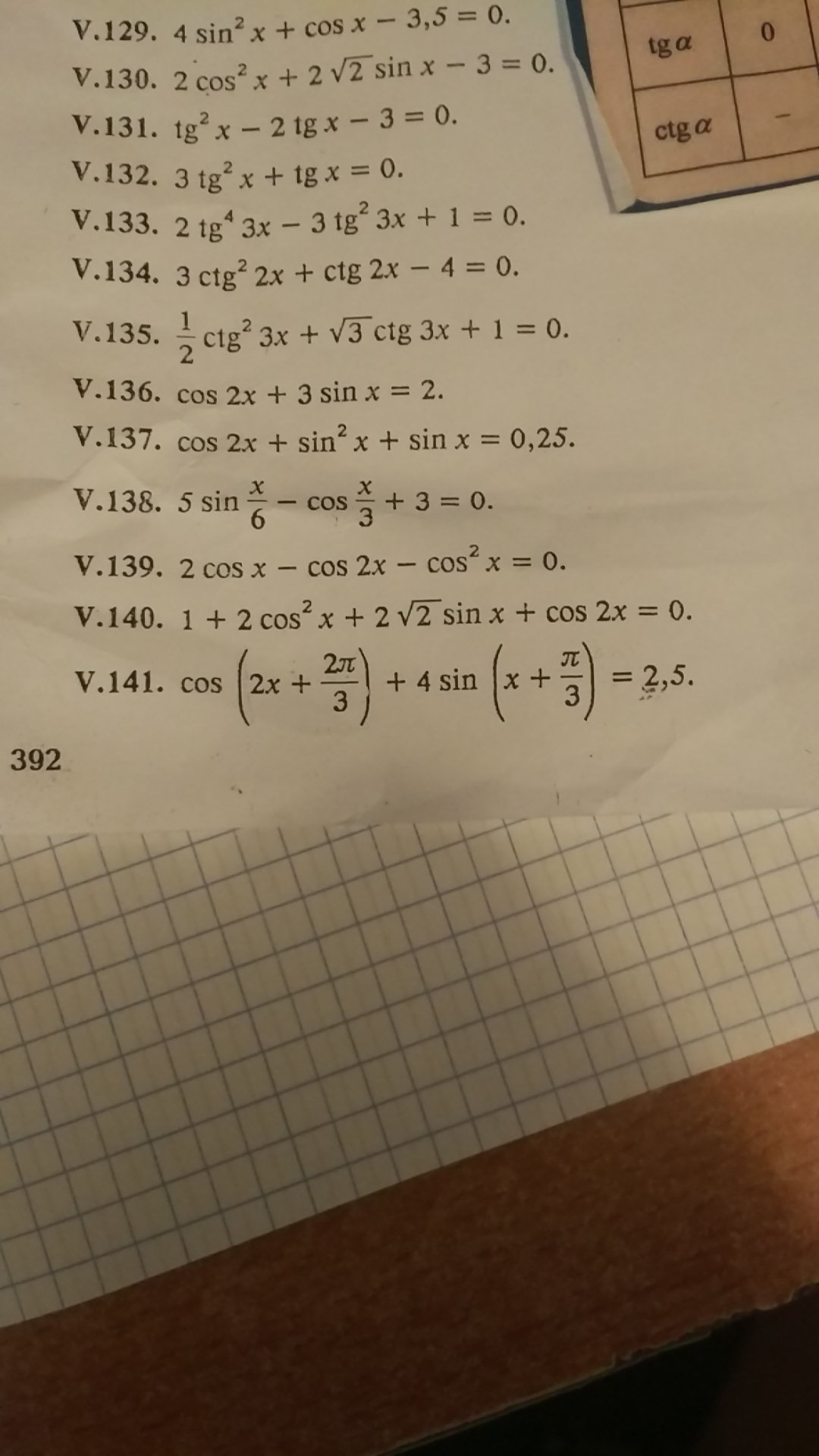
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: tttg86
Предмет: Физика,
автор: nastiabird
Предмет: Английский язык,
автор: galiakerim
Предмет: Математика,
автор: keermen2004
Предмет: Математика,
автор: nikolaygorshkov