Предмет: Алгебра,
автор: xachhfhfuFjd
Кто логарифмы знает помогите пожалуйста ответы вроде x=8;1/4 объясните ход решения пожалуйста
Приложения:
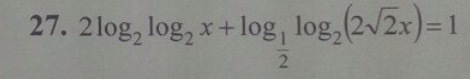
Ответы
Автор ответа:
0
ОДЗ:
Таким образом, корень 1/2 не подходит.
Ответ: 8.
Автор ответа:
0
Благодарствую
Автор ответа:
0
у тебя не правильно квадратная степень появояеться в иксе а в не самом логорифме
Автор ответа:
0
По свойству log(a)b^n=n*log(a)b степень 2 относится ко всему выражению log(2)x, а не только к х, т.е. (log(2)x)^2=log(2)x*log(2)x=log^2(2)x
Автор ответа:
0
Ошибка была в том, что я не проверила ОДЗ. Изменения внесены.
Похожие вопросы
Предмет: История,
автор: gameover2077
Предмет: Математика,
автор: oldbitmen
Предмет: Геометрия,
автор: elenamarkovskaya123
Предмет: Математика,
автор: ninanikova9
Предмет: Математика,
автор: bulatova31