Предмет: Алгебра,
автор: Nata980
Помогите пожалуйста доказать:
Приложения:
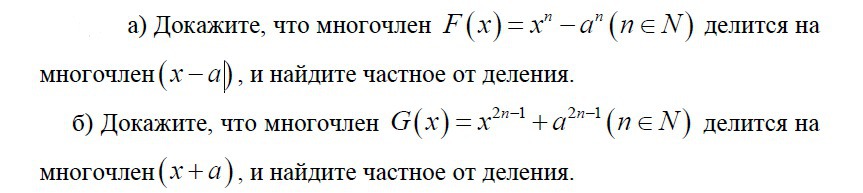
Ответы
Автор ответа:
0
Делимость очевидна в обоих случаях, так как многочлен и двучлен имеют общий корень x = a и x=-a соответственно. Частное найдем методом неопределенных коэффициентов

Если приравнять к нулю все коэффициенты, все получается. Начнем с того, что b1 = a, а остальные коэффициенты b2, b3 находятся по цепочке и получается

Вторую задачу решим аналогично

Опять приравняем все к 0 и получим
b1 = -a; b2 = a^2; b3 = -a^3... и слагаемых там ровно столько, что знаки в конце сойдутся, чтобы последнее слагаемое вышло -a^{2n-2}
Получим

Если приравнять к нулю все коэффициенты, все получается. Начнем с того, что b1 = a, а остальные коэффициенты b2, b3 находятся по цепочке и получается
Вторую задачу решим аналогично
Опять приравняем все к 0 и получим
b1 = -a; b2 = a^2; b3 = -a^3... и слагаемых там ровно столько, что знаки в конце сойдутся, чтобы последнее слагаемое вышло -a^{2n-2}
Получим
Автор ответа:
0
А, блин, это не на ту задачу ответ, я окно перепутал.
Автор ответа:
0
Пришлось и эту решить, теперь правильно
Похожие вопросы
Предмет: Геометрия,
автор: lizagorobec9
Предмет: Математика,
автор: mesumehaciyeva2008
Предмет: Русский язык,
автор: gaspar
Предмет: Литература,
автор: mardok762
Предмет: Математика,
автор: vadim2015egorov