Предмет: Алгебра,
автор: nastenka902
Помогите, пожалуйстаааа
Приложения:
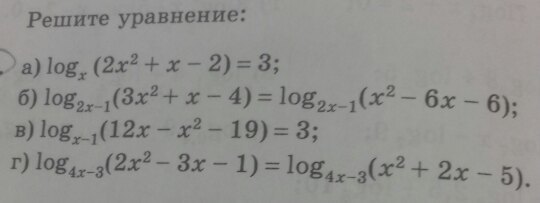
Ответы
Автор ответа:
0
Решите уравнения
а)
Решение
Область допустимых значений ОДЗ уравнения х > 0, x≠ 1


2x²+x-2 = x³
x³-2x²-x+2 = 0
x²(x-2)-(x-2) = 0
(x-2)(x²-1) = 0
x-2 = 0 x²-1=0
x = 2 (x-1)(x+1)=0
x=1 - не входит в ОДЗ
х=-1 - не входит в ОДЗ
Ответ: 2
б)
Решение
Область допустимых значений ОДЗ уравнения 2х-1> 0 или x>0,5, 2x-1≠ 1 или x≠1

3x² + x - 4 = x²- 6x - 6
2x² + 7x +2 = 0
D =7²-4*2*2 = 49 - 16
 не входит в ОДЗ так как меньше нуля
не входит в ОДЗ так как меньше нуля
 не входит в ОДЗ так как меньше нуля
не входит в ОДЗ так как меньше нуля
Ответ:∅
в)
Решение
Область допустимых значений ОДЗ уравнения х-1> 0 или x>1, x-1≠ 1 или x≠2


12x - x² - 19 = (x-1)³
12x - x² - 19 = x³ - 3x² + 3x - 1
x³ - 2x² - 9x +18 = 0
x²(x - 2) - 9(x - 2) = 0
(x² - 9)(x - 2) = 0
(x - 3)(x + 3)(x - 2) = 0
x = 3
x = -3 не входит в область ОДЗ
х = 2 не входит в область ОДЗ
Ответ: 3
г)
Решение
Область допустимых значений ОДЗ уравнения 4х-3> 0 или x>0,75, 4x-3≠ 1 или x≠1

2x² - 3x - 1 = x² + 2x - 5
x² - 5x + 4 = 0
D = 5² - 4*4 = 25 - 16 = 9
 не входит в ОДЗ
не входит в ОДЗ

Ответ: 4
а)
Решение
Область допустимых значений ОДЗ уравнения х > 0, x≠ 1
2x²+x-2 = x³
x³-2x²-x+2 = 0
x²(x-2)-(x-2) = 0
(x-2)(x²-1) = 0
x-2 = 0 x²-1=0
x = 2 (x-1)(x+1)=0
x=1 - не входит в ОДЗ
х=-1 - не входит в ОДЗ
Ответ: 2
б)
Решение
Область допустимых значений ОДЗ уравнения 2х-1> 0 или x>0,5, 2x-1≠ 1 или x≠1
3x² + x - 4 = x²- 6x - 6
2x² + 7x +2 = 0
D =7²-4*2*2 = 49 - 16
Ответ:∅
в)
Решение
Область допустимых значений ОДЗ уравнения х-1> 0 или x>1, x-1≠ 1 или x≠2
12x - x² - 19 = (x-1)³
12x - x² - 19 = x³ - 3x² + 3x - 1
x³ - 2x² - 9x +18 = 0
x²(x - 2) - 9(x - 2) = 0
(x² - 9)(x - 2) = 0
(x - 3)(x + 3)(x - 2) = 0
x = 3
x = -3 не входит в область ОДЗ
х = 2 не входит в область ОДЗ
Ответ: 3
г)
Решение
Область допустимых значений ОДЗ уравнения 4х-3> 0 или x>0,75, 4x-3≠ 1 или x≠1
2x² - 3x - 1 = x² + 2x - 5
x² - 5x + 4 = 0
D = 5² - 4*4 = 25 - 16 = 9
Ответ: 4
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: ОБЖ,
автор: lerazero101019
Предмет: Математика,
автор: Anarxist352
Предмет: Математика,
автор: lyudmila28
Предмет: Математика,
автор: livshit