Предмет: Алгебра,
автор: alexeiz381
2*7^x7^2x-1>=7x7x-1-17x+1
Приложения:
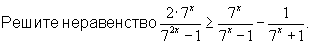
Ответы
Автор ответа:
0
Не имеет решений. ( только при
, но у нас рассматриваются
)
Похожие вопросы
Предмет: Математика,
автор: Ducj000
Предмет: Математика,
автор: WASDEGT
Предмет: Английский язык,
автор: AlisaYvarova
Предмет: Математика,
автор: 375333454240