Предмет: Алгебра,
автор: СтасЕфремов
Решите кто сможет...................................
Приложения:
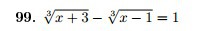
Ответы
Автор ответа:
0
......................
Приложения:

Автор ответа:
0
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: 16022006zhasmin
Предмет: Математика,
автор: sabunaaltaeva19gj
Предмет: Математика,
автор: OhhMyGlob
Предмет: Математика,
автор: altynbaeva2014