Найдите область определения функции: a) y=1/3x-4; б) y= x+1/(x-2)(x+3); в) у= х/ х2-9х+14; г)у= под корнем: 2x+5
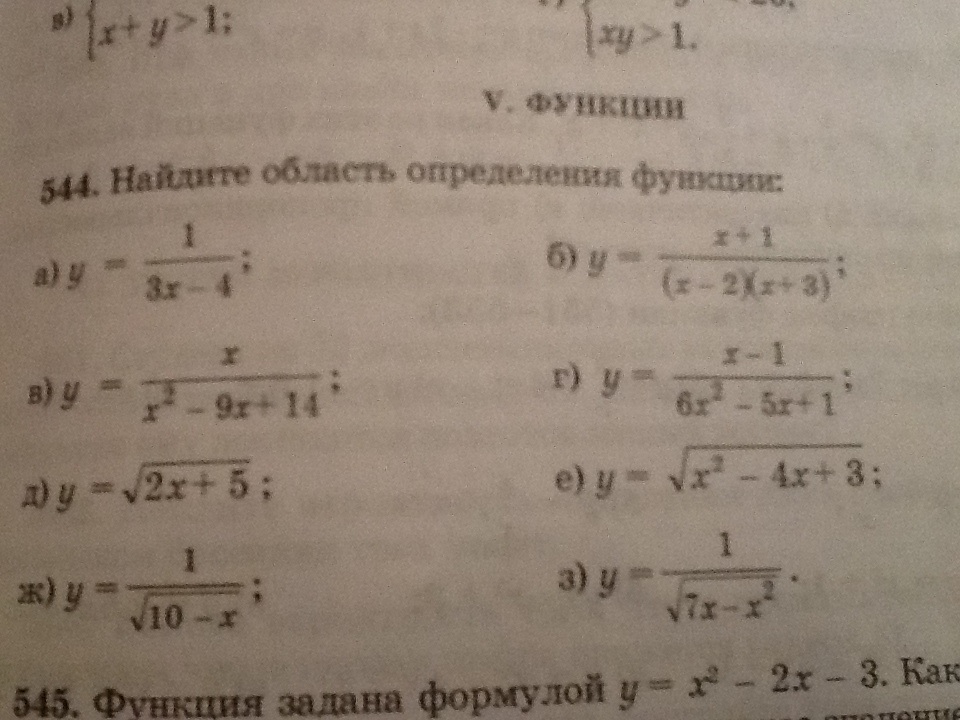
Ответы
Область определения функции - это множество чисел, на котором задается функция.
Другими словами, это те значения х, которые можно подставить в данное уравнение и оно не потеряет смысла
а)
Выражение содержит дробь. Значит знаменатель не должен равнятся нулю
3х-4≠0; 3х≠4; х≠4/3
Область определения: (-∞;4/3)∪(4/3;+∞)
б)
Выражение содержит дробь. Значит знаменатель не должен равнятся нулю
(x-2)(x+3)≠0; x≠2 и x≠-3
Область опреления: (-∞;-3)∪(-3;2)∪(2;+∞)
в)
Выражение содержит дробь. Значит знаменатель не должен равнятся нулю
x²-9x+14≠0; (x-7)(x-2)≠0; x≠7 и x≠2
Область опредения: (-∞;2)∪(2;7)∪(7;+∞)
г)
Выражение содержит дробь. Значит знаменатель не должен равнятся нулю
6x²-5x+1≠0; (2x-1)(3x-1)≠0; x≠1/2 и x≠1/3
Область определения: (-∞;1/3)∪(1/3;1/2)∪(1/2;+∞)
д)
Выражение содержит квадратный корень, Значит подкоренное выражение должно быть не отрицательным
2x+5≥0; 2x≥ -5; x≥ -2.5
Область определения: [-2.5; +∞)
e)
Выражение содержит квадратный корень, Значит подкоренное выражение должно быть не отрицательным
x²-4x+3≥0
(x-3)(x-1)≥0
Область опредения: (-∞;1]∪[3;+∞)
ж)
Выражение содержит квадратный корень и дробь, Значит подкоренное выражение должно быть положительным
10-x>0; x<10
Область определения: (-∞;10)
з)
Выражение содержит квадратный корень и дробь, Значит подкоренное выражение должно быть положительным
7x-x²>0; x(7-x)>0
Область определения: (0;7)