Предмет: Алгебра,
автор: khitrovatanya
ПОМОГИТЕ НАЙТИ ПРЕДЕЛ ФУНКЦИИ ПОЖАЛУЙСТА
ОЧЕНЬ НАДО
Приложения:
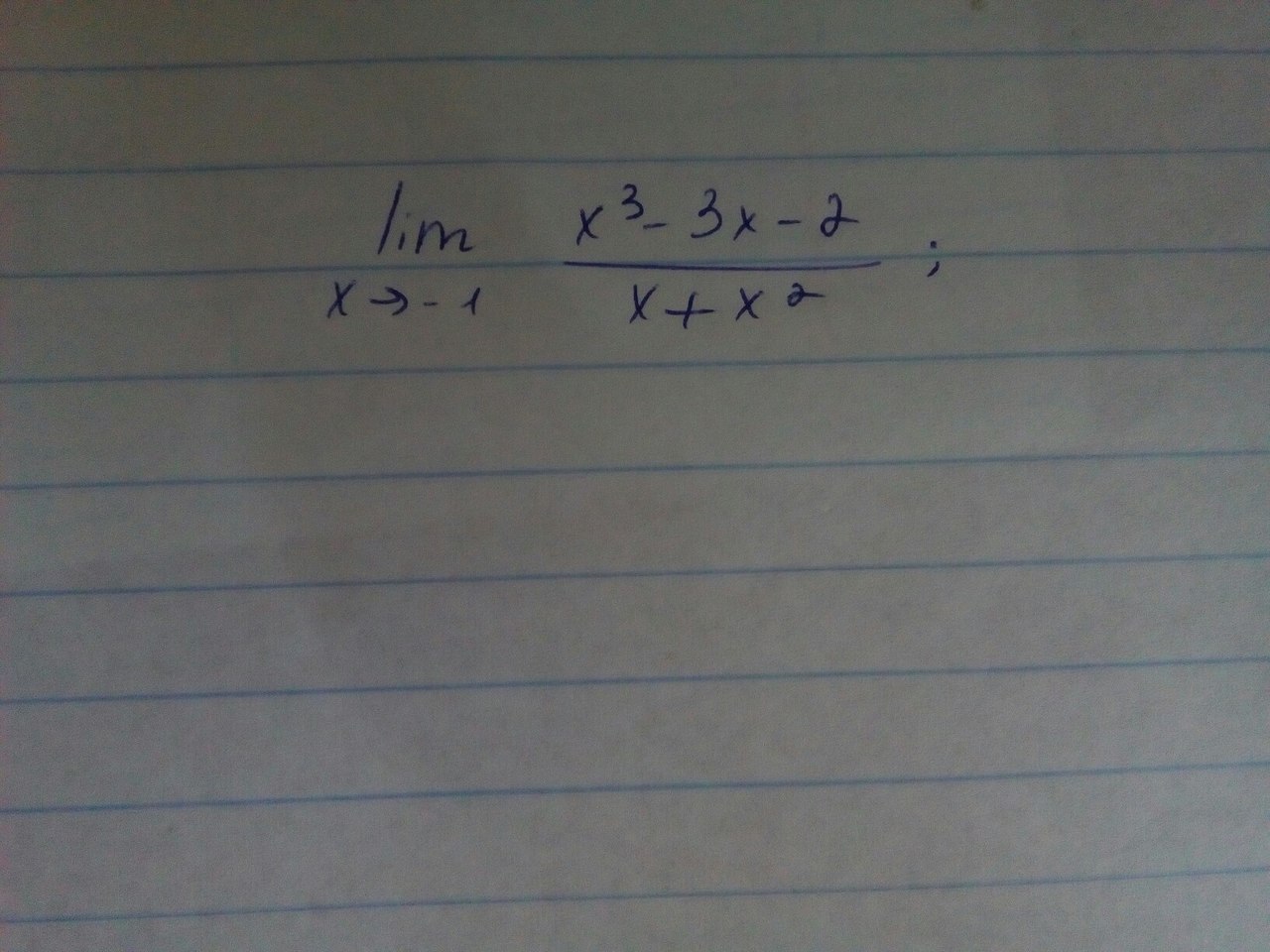
Ответы
Автор ответа:
0
производная от числителя равна 3х²-3
производная от знаменателя равна 2х+1
Воспользуемся правилом Лопиталя еще раз:
вторая производная от числителя: 6х
вторая производная от знаменателя: 2
Получается предел от (6х)/2=3х при х стремящимся к минус 1 будет стремиться к минус трем
производная от знаменателя равна 2х+1
Воспользуемся правилом Лопиталя еще раз:
вторая производная от числителя: 6х
вторая производная от знаменателя: 2
Получается предел от (6х)/2=3х при х стремящимся к минус 1 будет стремиться к минус трем
Автор ответа:
0
спасибо)
Автор ответа:
0
кстати, был не прав. Второй раз не надо было правило Лопиталя применять. Уже с первого раза предел можно было вычислить
Автор ответа:
0
у вас время сейчас есть?
Автор ответа:
0
Решение
Применим правило Лопиталя: ( предел отношения функций равен пределу отношения их производных).
lim x--> - 1 (f`(x) / g`(x))
Найдём производные:
f'(x) = 3x² - 3
g'(x) = 2x + 1
подставим в формулу:
lim x -- > - 1 [(3x² - 3)/(2x + 1)] = (3*(-1)² - 3)/(2*(-1) + 1) = 0/(-1) = 0
Применим правило Лопиталя: ( предел отношения функций равен пределу отношения их производных).
lim x--> - 1 (f`(x) / g`(x))
Найдём производные:
f'(x) = 3x² - 3
g'(x) = 2x + 1
подставим в формулу:
lim x -- > - 1 [(3x² - 3)/(2x + 1)] = (3*(-1)² - 3)/(2*(-1) + 1) = 0/(-1) = 0
Автор ответа:
0
спасибо)
Автор ответа:
0
тут такое дело, нужно 10 заданий решить, где пределы, дифференциалы, производные и интегралы, очень нужно, сможете помочь?
Автор ответа:
0
буду создавать отдельное задание для каждого
Похожие вопросы
Предмет: Українська література,
автор: Аноним
Предмет: Английский язык,
автор: VPod73
Предмет: Русский язык,
автор: kurbanovaelina10
Предмет: Математика,
автор: nikazali12