Предмет: Геометрия,
автор: nastiOpHukol
Выполнить 3 задания ,даю 100 баллов.
Приложения:
Ответы
Автор ответа:
0
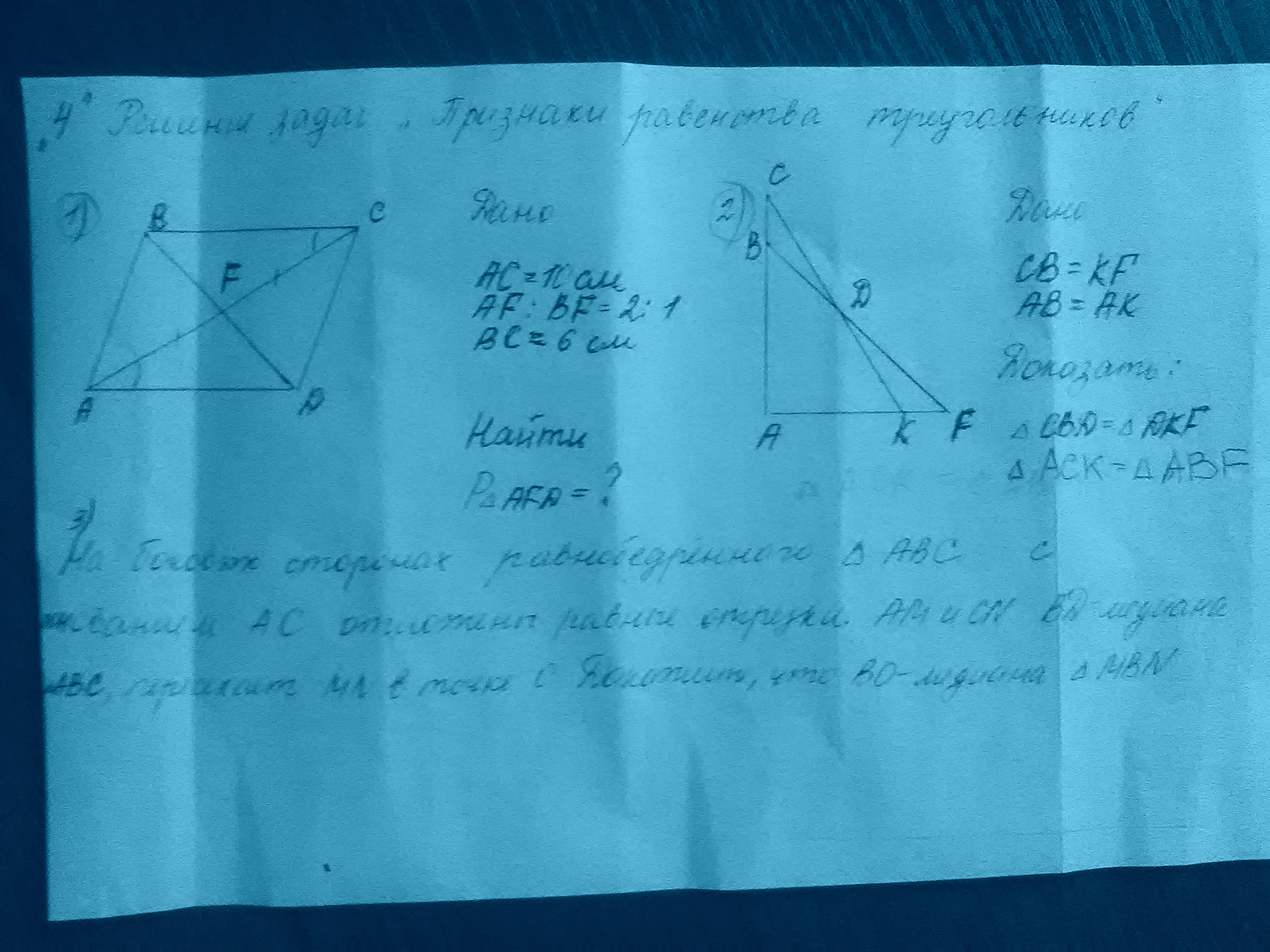
1.
Углы BCF и FAD равны по условию
AF=FC по условию
Углы DFC и AFD равны как вертикальные углы при пересечении прямых AC и BD.
Следовательно, треугольники AFD и BFC равны по двум углам и стороне между ними (2-ой признак равенства треугольников)
Pafd=Pbfc
BF=5/2=2,5см
P=6+5+2,5=13,5см
Ответ: 13,5
2.
AB=AK по условию
AC=AF (AB=AK + BC=KF по условию)
Угол A - общий
Следовательно, треугольники ACK и ABF равны по двум сторонам и углу между ними (1-ый признак равенства треугольников)
Из прежде доказанного равенства треугольников ABF и ACK следует, что углы ACK и BFA, CBF и FKC равны
BC=KF по условию
Следовательно, треугольники BCD и KDF равны по двум углам и стороне между ними (2-ой признак равенства треугольников)
3.
В равнобедренном треугольнике медиана, исходящая из угла не при основании является еще и высотой, биссектрисой.
Углы MBO и OBN равны (свойство биссектрисы)
MB=BN (AB=BC + AM=NC по условию)
BO - общая сторона
Следовательно, треугольники MBO и OBN равны по двум сторонам и углу между ними (1-ый признак равенства треугольников)
Отсюда равенство отрезков MO и ON, доказывающее, что BO - медиана.
Углы BCF и FAD равны по условию
AF=FC по условию
Углы DFC и AFD равны как вертикальные углы при пересечении прямых AC и BD.
Следовательно, треугольники AFD и BFC равны по двум углам и стороне между ними (2-ой признак равенства треугольников)
Pafd=Pbfc
BF=5/2=2,5см
P=6+5+2,5=13,5см
Ответ: 13,5
2.
AB=AK по условию
AC=AF (AB=AK + BC=KF по условию)
Угол A - общий
Следовательно, треугольники ACK и ABF равны по двум сторонам и углу между ними (1-ый признак равенства треугольников)
Из прежде доказанного равенства треугольников ABF и ACK следует, что углы ACK и BFA, CBF и FKC равны
BC=KF по условию
Следовательно, треугольники BCD и KDF равны по двум углам и стороне между ними (2-ой признак равенства треугольников)
3.
В равнобедренном треугольнике медиана, исходящая из угла не при основании является еще и высотой, биссектрисой.
Углы MBO и OBN равны (свойство биссектрисы)
MB=BN (AB=BC + AM=NC по условию)
BO - общая сторона
Следовательно, треугольники MBO и OBN равны по двум сторонам и углу между ними (1-ый признак равенства треугольников)
Отсюда равенство отрезков MO и ON, доказывающее, что BO - медиана.
Похожие вопросы
Предмет: Українська мова,
автор: alhgfdryu
Предмет: Українська мова,
автор: klaradeola14
Предмет: Информатика,
автор: sosnznx
Предмет: Алгебра,
автор: данич98
Предмет: Информатика,
автор: OtveTnoy