Предмет: Геометрия,
автор: Elizabeth13111
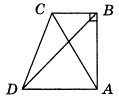
20 баллов ;) На рисунке ABCD — прямоугольная трапеция, площадь которой равна 8 см2. Площадь треугольника ADB равна 5 см2. Тогда площадь треугольника ABC равна
Приложения:
Ответы
Автор ответа:
0
Площадь прямоугольной трапеции АВСД равна сумме площадей треугольников АДВ и ДСВ.
Площадь треугольника АДВ известна, она равна 5 см^2.
Площадь трапеции АВСД тоже известна; она равна 8 см^2.
Значит, площадь треугольника ДСВ равна 8-5=3 см^2.
Площади треугольников ДСВ и АВС равны; докажем это.
Сделаем дополнительное построение.
Проведём из вершины Д отрезок ДК параллельно АВ до пересечения с продолжением ВС.
ДК равно АВ, так как АДКВ прямоугольник (все углы прямые).
ДК - это высота треугольника ДСВ.
Площадь треугольника равна половине произведения основания на высоту.
У треугольников ДСВ и АВС основание ВС общее, а высоты ДК и АВ равны.
Значит, площадь треугольника АВС равна площади треугольника ДСВ и равна 3 см^2.
Ответ: 3
Похожие вопросы
Предмет: История,
автор: isatsoi
Предмет: Математика,
автор: ZokirloxIlox
Предмет: Химия,
автор: wrrdxs
Предмет: Алгебра,
автор: veronika1409199
Предмет: Информатика,
автор: max99932