Question

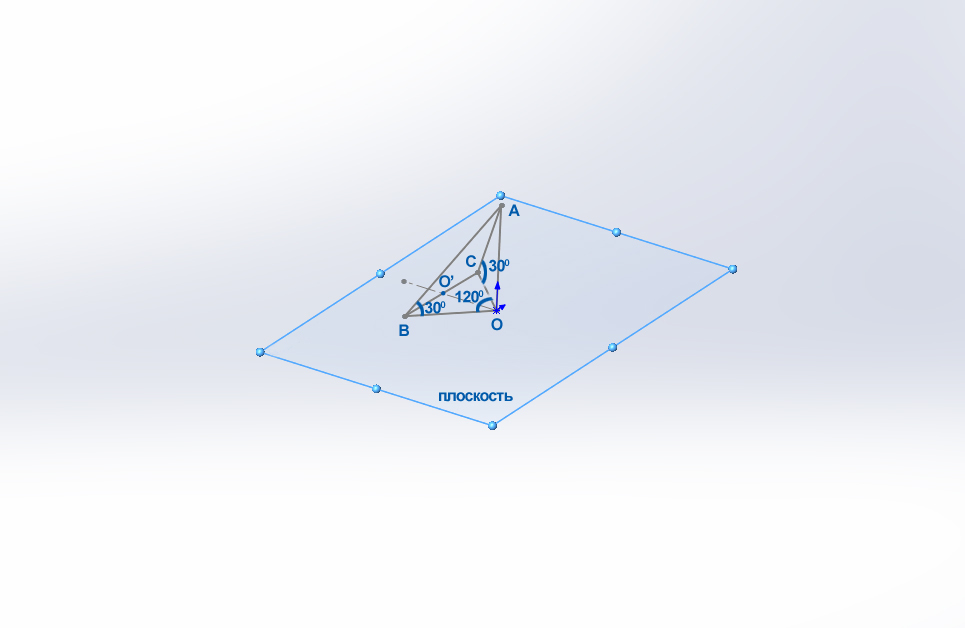
Из точки А, удаленной от плоскости γ на расстояние d, проведены к этой плоскости наклонные АВ и АС под углом 30° к плоскости. Их проекции на плоскость γ образуют угол в 120°. Найдите ВС. РЕШИТЕ БЕЗ ТЕОРЕМЫ КОСИНУСОВ.

Answer 1

Так как ∠ABO=∠ACO, то BO=BC, а треугольник COB равнобедренный
Найдем BO
tg30°=$frac{AO}{BO}$ ⇒ BO=$frac{d}{tg30}$=d√3 условных единиц длины
Т.к треугольник COB равнобедренный, то СO'=BO'; BC=2BO'
Найдем BO'
Sin60°=$frac{BO'}{BO}$ ⇒ BO'=d√3*√3/2=$frac{3d}{2}$ условных единиц длины
Соответственное BC=$frac{2*3*d}{2}=3d$

Answer 2

у меня вопрос: почему ∠ABO=∠ACO?

Answer 3

потому что АО перпендикулярно плоскости и... точки B и С симметричны относительно ОО'

Answer 4

Что это за теорема или правило?

Answer 5

Это не теорема и не правило, это следует из условия "Их проекции на плоскость γ образуют угол в 120°" при этом "проведены к этой плоскости наклонные АВ и АС под углом 30° к плоскости" Раз проведены из одной точки под одинаковым углом к плоскости то длины проекций будут равны

Answer 6

Спасибо!