Предмет: Математика,
автор: janabbb
Решите, пожалуйста, логарифмическое неравенство! ОЧЕНЬ ПРОШУ!
log0,5 ( (x^2+x) )>-1
Приложения:
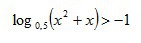
Ответы
Автор ответа:
0
Применены свойства логарифмов
Приложения:

Автор ответа:
0
+ - +
---------o----------o---------->x
-2 1
под логарифмом не может быть значение меньше 0, поэтому
x²+x>0
x(x+1)>0
+ - +
---------o----------o---------->x
-1 0
Объединив эти 2 значения, определяем пересечения
x∈(-2;-1)∪(0;1)
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: KaLaChlol
Предмет: Английский язык,
автор: alenaburnats
Предмет: Қазақ тiлi,
автор: spotlightkiler
Предмет: Физика,
автор: azandr99