Question

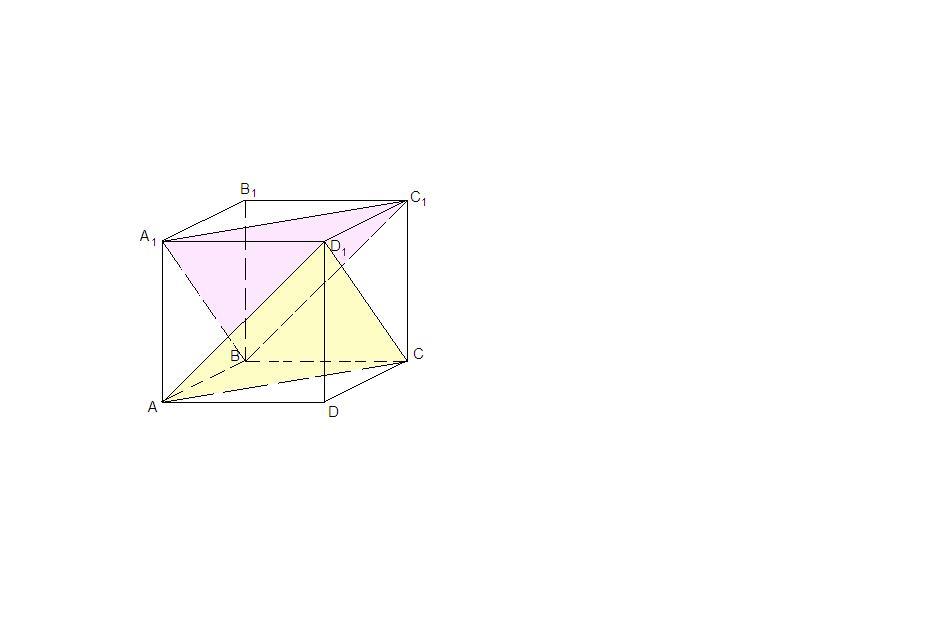
В кубе ABCDA1B1C1D1 укажите плоскость, параллельную плоскости A1BC1 и проходящую через три вершины куба.

Answer 1

Ответ:

AD₁C

Объяснение:

AA₁ = BB₁ и AA₁║BB₁, a BB₁ = CC₁ и BB₁║CC₁ как противоположные стороны квадратов, значит

AA₁║CC₁ и АА₁ = СС₁,  значит

АА₁С₁С - параллелограмм, ⇒

АС ║ А₁С₁

Аналогично, A₁D₁ = BC и A₁D₁║BC, значит

A₁D₁CB - параллелограмм, ⇒

A₁B║D₁C

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

AD₁C ║ A₁BC₁