Question

Один из острых углов прямоугольного треугольника в два раза меньше другого а разность гипотенузы и меньшего катета равна 15 см Найдите гипотенузу и меньший катет

Answer 1

Пусть АВС - прямоугольный треугольник, угол С=90 градусов.

Пусть угол А=х, тогда В=2х.

х+2х=90

3х=90

х=30

А=30, В=60.

В прямоугольном треугольнике катет, лежащий  против угла 30 градусов, равен половине гипотенузы. И еще против меньшего острого угла лежит меньший катет.

Пусть катет СВ=y см, тогда гипотенуза АВ=15+у см.

15+у=2у

у=15

СВ=15 см, АВ=30 см. 

Answer 2

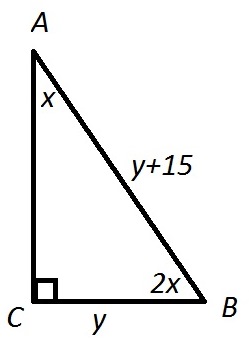
Пусть один угол навен у градусов, тогда второй 2у градусов. Т.к. треугольник прямоугольный то у+2у=90 следоватьльно у=30 следовательно один угол равен 30 градусов другой 60. 

Пусть меньший катет равен х, а гипотенуза х+15, т.к. угол =30 градусов то катет лежащий против угла в 30 градусов в два раза меньше гипотенузы, следовательно

х=(15+х)/2

2х=15+х

х=1меньший катет равен 15 см, гипотенуза 30 см