Question

Найти площадь фигуры, ограниченный график функции
у=x^2+4x+5 и прямыми
х=-1 и x=2 и осью абсциссе

Answer 1

Чтобы найти площадь, нужно сначала построить фигуру
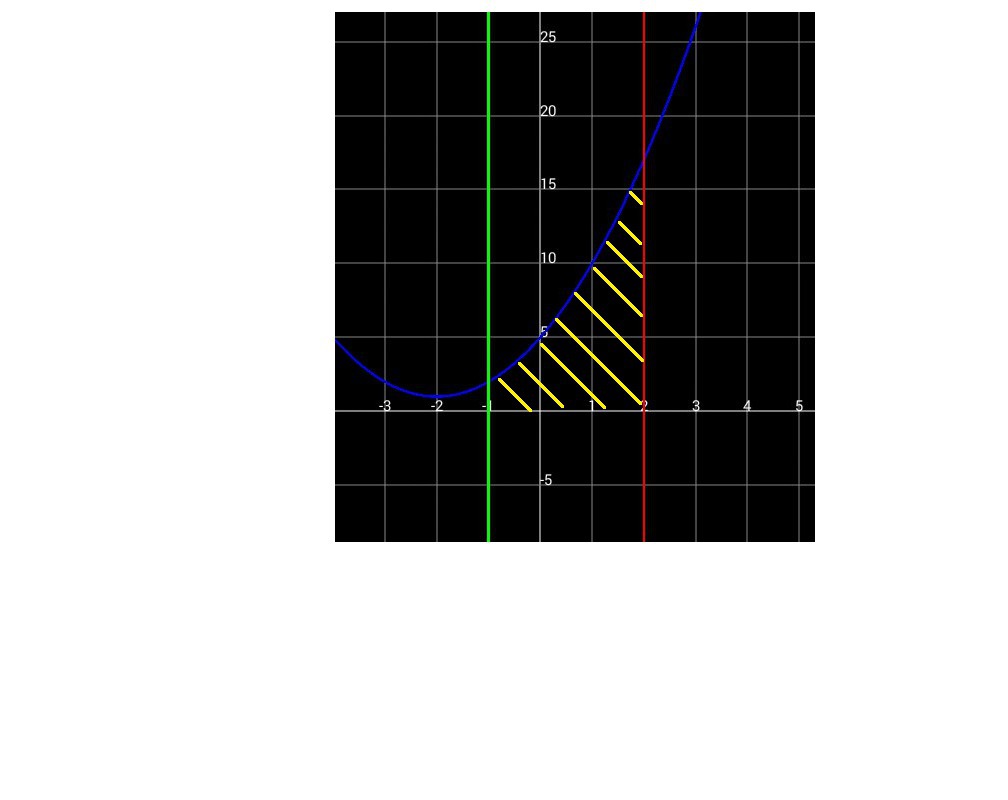
Строим по точкам параболу: у=x²+4x+5 (синий график)
и две вертикальные прямые: х=-1 и х=2  (зеленый и красный графики).
Ось абсцисс-это ось ОХ.

Результатом пересечения является криволинейная трапеция (заштрихованная желтая фигура), которая находится в области (по иксу) от -1 до 2

Площадь криволинейной трапеции равен определенному интегралу кривой на области интегрирования от -1 до 2

$intlimits^2_{-1} {(x^2+4x+5)} , dx = frac{x^3}{3} +4* frac{x^2}{2} +5x=frac{x^3}{3} +2x^2 +5x |_{-1} ^2= \ \ frac{2^3}{3} +2*2^2 +5*2-(frac{(-1)^3}{3} +2(-1)^2 +5(-1))= \ \ = frac{8}{3} +8+10-(- frac{1}{3} +2-5)=frac{8}{3} +8+10+ frac{1}{3} -2+5=24 \ \ OTBET: 24$