Предмет: Алгебра,
автор: SaDpInGvIn
сложное тригонометрическое уравнение .
Приложения:
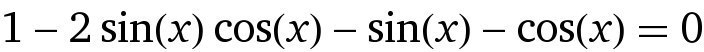
Ответы
Автор ответа:
0
Ответ ₩¥£€€¥₩¥€_€¥₩¥_% €£¥¥_%
Приложения:

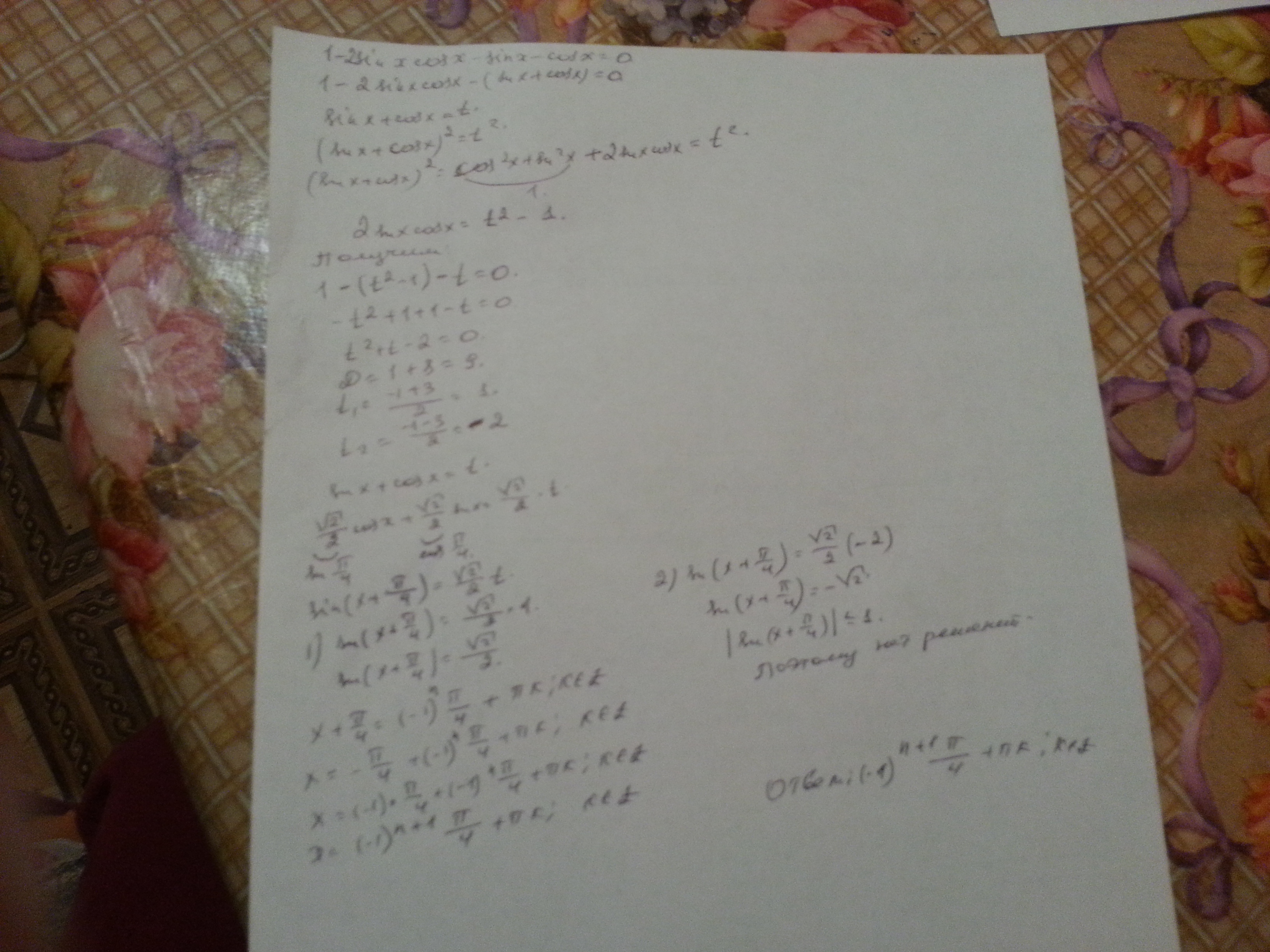
Автор ответа:
0
Вместе к везде п
Автор ответа:
0
Вынести П/4, а в скобках будет (-1+(-1)^{n}). Не получится (-1)^{n+1}.
Автор ответа:
0
Последних 2 строк не надо было, надо было дать п=2к и п=2к+1.тогда получается правильно
Автор ответа:
0
Получается 2пи n и пи/2+2пи n.
Автор ответа:
0
Да
Автор ответа:
0
Приложения:

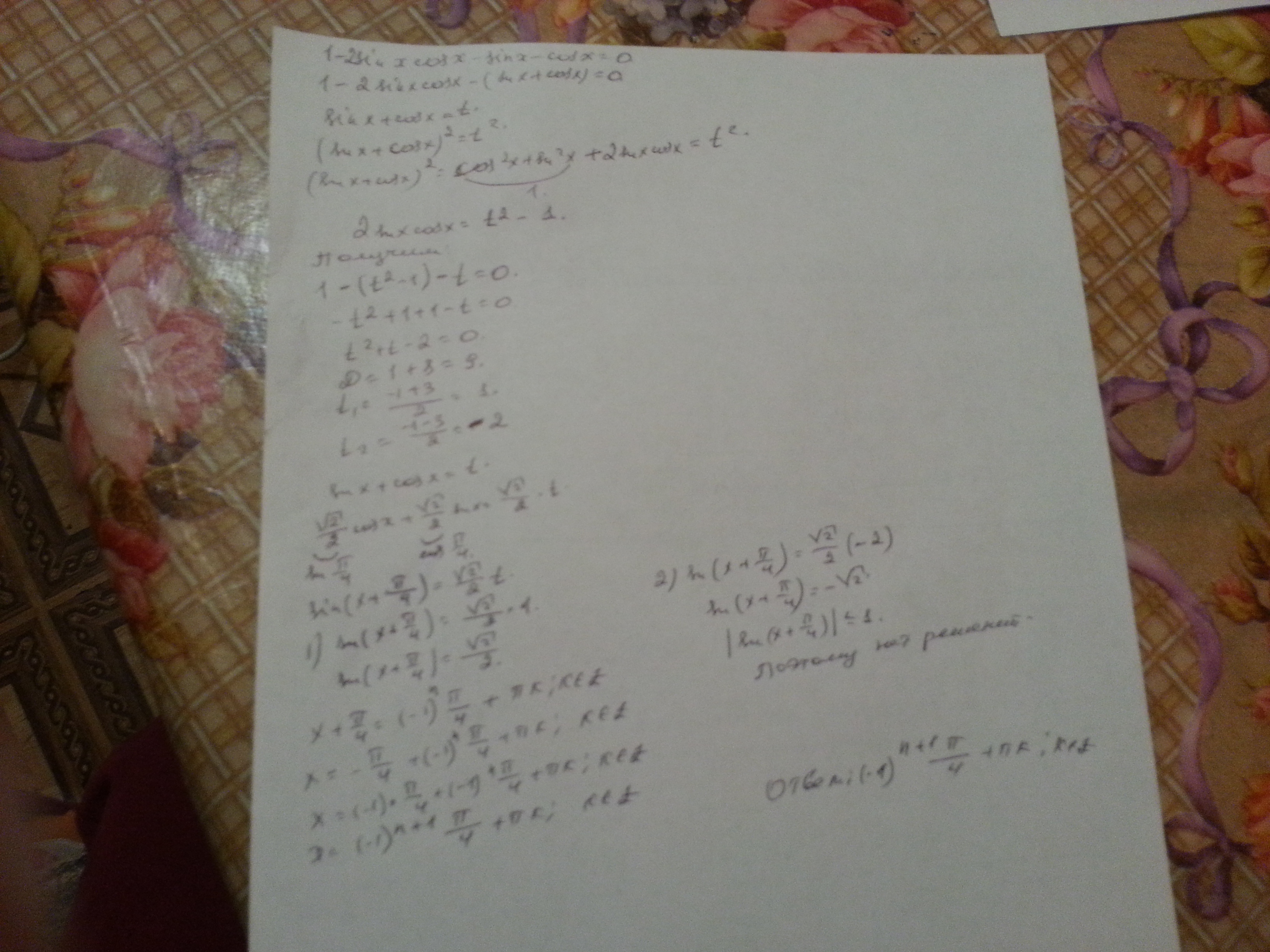
Автор ответа:
0
Спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: anaiskhud1
Предмет: Математика,
автор: annablohina59
Предмет: Английский язык,
автор: seitovazhasmin09
Предмет: Математика,
автор: veraillarionovq