Предмет: Математика,
автор: wiktoria12
Помогите пожалуйста, найти интеграл.
Приложения:
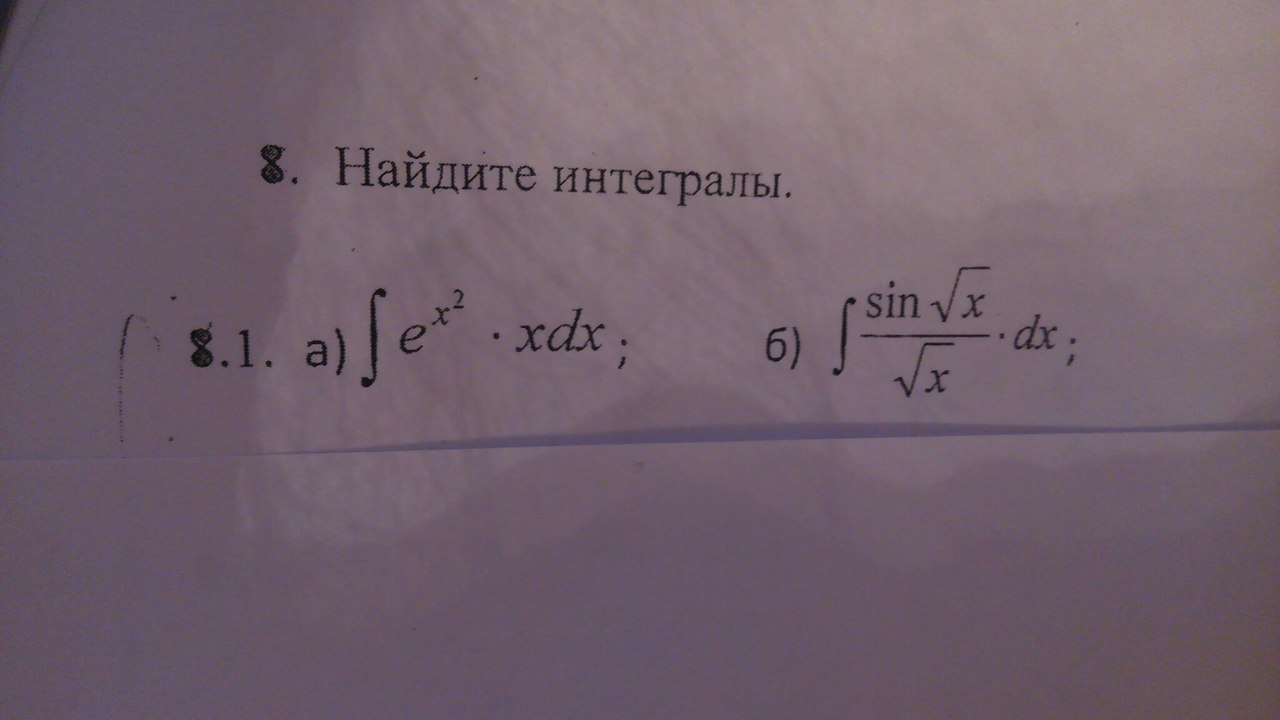
Ответы
Автор ответа:
0
смотри, 2 метода для буквы а)
№1 метод
пусть u=x2u=x2 .Тогда пусть du=2xdxdu=2xdx и подставим du2du2 :∫eudu∫eudu Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:∫eudu=12∫eudu∫eudu=12∫eudu Интеграл от экспоненты есть он же сам.∫eudu=eu∫eudu=eu Таким образом, результат будет: eu2eu2 Если сейчас заменить uu ещё в:ex22ex22 Метод #2Перепишите подынтегральное выражение:ex2x=xex2ex2x=xex2 пусть u=x2u=x2 .Тогда пусть du=2xdxdu=2xdx и подставим du2du2 :∫eudu∫eudu Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:∫eudu=12∫eudu∫eudu=12∫eudu Интеграл от экспоненты есть он же сам.∫eudu=eu∫eudu=eu Таким образом, результат будет: eu2eu2 Если сейчас заменить uu ещё в:ex22ex22 Добавляем постоянную интегрирования:ex22+constantex22+constant
№1 метод
пусть u=x2u=x2 .Тогда пусть du=2xdxdu=2xdx и подставим du2du2 :∫eudu∫eudu Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:∫eudu=12∫eudu∫eudu=12∫eudu Интеграл от экспоненты есть он же сам.∫eudu=eu∫eudu=eu Таким образом, результат будет: eu2eu2 Если сейчас заменить uu ещё в:ex22ex22 Метод #2Перепишите подынтегральное выражение:ex2x=xex2ex2x=xex2 пусть u=x2u=x2 .Тогда пусть du=2xdxdu=2xdx и подставим du2du2 :∫eudu∫eudu Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:∫eudu=12∫eudu∫eudu=12∫eudu Интеграл от экспоненты есть он же сам.∫eudu=eu∫eudu=eu Таким образом, результат будет: eu2eu2 Если сейчас заменить uu ещё в:ex22ex22 Добавляем постоянную интегрирования:ex22+constantex22+constant
Ответ:
ex22+constantex22+constant
а с б помочь не смогу:(
Автор ответа:
0
спасибо большое!
Автор ответа:
0
пожалуйста! но почему лучшее решение -- решение другого человека? :(
Автор ответа:
0
Решение
Интегрируемое выражение:
((sin((sqrt(x)))))/((sqrt(x)))((sin((sqrt(x)))))/((sqrt(x)))
Есть несколько способов вычислить этот интеграл.
Способ 1
Пусть u=x−−√u=x.
Теперь пусть du=dx2x√du=dx2x. Заменим 2du2du:
∫sin(u)du∫sin(u)du
Выносим множитель за знак интегрирования:
∫sin(u)du=2∫sin(u)du∫sin(u)du=2∫sin(u)du
Интеграл синуса равен минус косинусу:
∫sin(u)du=−cos(u)∫sin(u)du=−cos(u)
Итак, результат: −2cos(u)−2cos(u)
Теперь подставляем uu обратно:
−2cos(x−−√)−2cos(x)
Способ 2
Перепишем подынтегральное выражение:
1x−−√sin(x−−√)=1x−−√sin(x−−√)1xsin(x)=1xsin(x)
Пусть u=x−−√u=x.
Теперь пусть du=dx2x√du=dx2x. Заменим 2du2du:
∫sin(u)du∫sin(u)du
Выносим множитель за знак интегрирования:
∫sin(u)du=2∫sin(u)du∫sin(u)du=2∫sin(u)du
Интеграл синуса равен минус косинусу:
∫sin(u)du=−cos(u)∫sin(u)du=−cos(u)
Итак, результат: −2cos(u)−2cos(u)
Теперь подставляем uu обратно:
−2cos(x−−√)−2cos(x)
Добавляем постоянную интегрирования:
−2cos(x−−√)+constant−2cos(x)+constant
Ответ:
−2cos(x−−√)+constant−2cos(x)+constant
Похожие вопросы
Предмет: Математика,
автор: tattygulturatbekkyzy
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: rouzalina199086
Предмет: Математика,
автор: regenok
Предмет: Алгебра,
автор: dio35