5. В кубе ABCDA1B1C1D1 с ребром , равным 1, проведено сечение MNK,
где точка М – середина ребра AD, точка N лежит на ребре АВ так,
что AN : NB = 1 : 3, точка К – на ребре АА1 такая, что АК : КА1= 1 : 4.
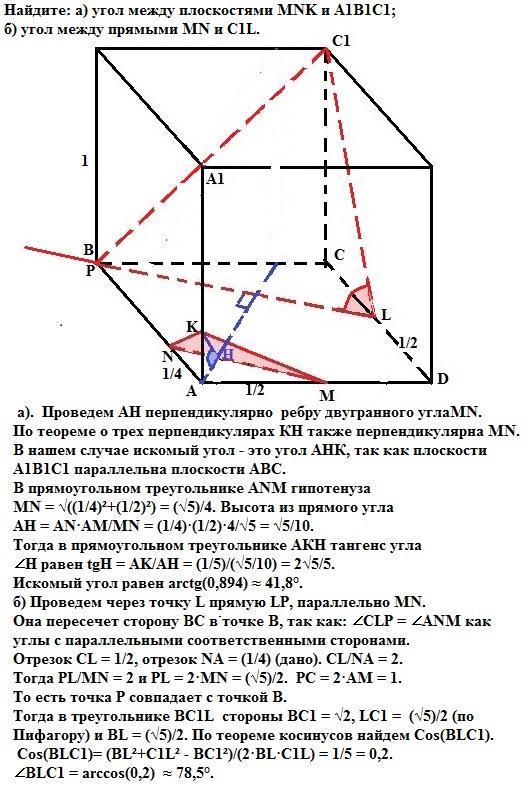
Найдите: а) угол между плоскостями MNK и А1В1С1;
б) расстояние и угол между прямыми MN и С1L, где L – середина ребра DC.
Ответы
как я тебе и говорил решение долгое и нудное.-_-
По определению углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Проведём прямую паралельную MN, через точку L и доведём её до пересечения с продолжением AB. Пусть эта точка будет N1.
Тогда угол C1LN1 искомый угол между прямыми. Обозначим его через х.
Найдём все стороны данного треугольника.
Теперь через теормему косинусов найдём угол.
Расстояние между прямыми С1L и NM будет равно расстояни NM и N1L. Проведи перпедикуля из точки N или M к прямой LN1. И найди его длинну. Я не успеваю извини. Сам найдёшь?
Ответ:
а) arctg(2√5/5) = arctg(0,894) ≈ 41,8°.
б) Расстояние между прямыми MN и С1L равно √6/4 ≈ 0,61
Угол (MN^C1L) = arccos(0,2) ≈ 78,5°.
Объяснение:
а). Цитата: "Угол между двумя пересекающимися плоскостями - это двугранный угол. Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Величина угла между пересекающимися плоскостями принадлежит промежутку (0;90°)".
Проведем АН перпендикулярно ребру двугранного угла MN. По теореме о трех перпендикулярах КН также перпендикулярна MN. В нашем случае искомый угол - это угол АНК, так как плоскости А1В1С1 параллельна плоскости АВС.
В прямоугольном треугольнике АNM гипотенуза
MN = √((1/4)²+(1/2)²) = (√5)/4. Высота из прямого угла
АН = AN·AM/MN = (1/4)·(1/2)·4/√5 = √5/10.
Тогда в прямоугольном треугольнике АКН тангенс угла ∠Н равен
tgH = AK/AH = (1/5)/(√5/10) = 2√5/5.
Искомый угол равен arctg(2√5/5) =arctg(0,894) ≈ 41,8°.
Координатный метод:
Точки К(0;0;1.5), М(0;1/2;0), N(1/4;0;0).
Уравнение плоскости А1В1С1, параллельной плоскости x0y^ z = 1,
Уравнение в общем виде: 0·x +0·y +1·z -1 = 0, с коэффициентами А=0, В=0, С=1, D=-1.
Уравнение плоскости MNK получим через определитель:
| x-0 y-0 z-1 |
| 0 1/2 -1/5 | = 0. Или (-1/10)·x - (1/20)·y + (-1/8)·z +1/40 = 0.
| 1/4 0 -1/5 |
То есть коэффициенты А= -1/10, В = -1/20, С = -1/8б D = 1/40.
По формуле:
Cosa = |0+0-1/8|/((√(0+0+1)·√(1/100+1/400+1/64)) = 80·10/(8√180) или
Cosa = 10/√180 = 3√20/18 = √5/3 ≈ 0,745.
a = arccos(0,745) ≈ 41,8°
б). Прямые MN и LC1 - скрещивающиеся прямые. Углом между скрещивающимися прямыми является угол между пересекающимися прямыми, параллельными данным скрещивающимся. Проведем через точку L прямую LP, параллельно MN.
Она пересечет сторону ВС в точке В, так как:
∠СLP = ∠ANM как углы с параллельными соответственными сторонами. Отрезок CL = 1/2, отрезок NA = (1/4). CL/NA = 2. Тогда PL/MN = 2 и PL = 2·MN = (√5)/2. PC = 2·AM = 1. То есть точка Р совпадает с точкой В.
Проверка: точки М((1/2;0;0;) и N(0;1/4;0) => вектора MN и LB коллинеарны, так как отношения соответствующих координат равны: MN{-1/2;1/4;0} и LB{-1;1/2;0}.
Отношения для х: =1/2, для y: 1/2.
Тогда в треугольнике ВС1L стороны ВС1 = √2, LC1 = (√5)/2 (по Пифагору) и BL = (√5)/2. По теореме косинусов найдем Cos(BLC1).
Cos(BLC1)= (BL²+C1L² - BC1²)/(2·BL·C1L) = 1/5 = 0,2.
∠BLC1 = arccos(0,2) ≈ 78,5°.
Координатный метод:
Вектор MN={1/4;-1/2;0}. |MN| = √(1/16+1/4+0) = √5/4.
Вектор С1L={-1/2;0;-1}. |C1L| = √(1/4+0+4/4) = √5/2.
Cos(MN^C1L) = |(-1/8 +0+0)|/(√5/4)² = (1/8)·(8/5) = 1/5 = 0,2.
(MN^C1L) = arccos(0,2) ≈ 78,5°.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой. В нашем случае это плоскость BC1L , так как прямая BL, принадлежащая этой плоскости параллельна прямой MN (доказано выше).
В прямоугольном треугольнике ANM гипотенуза NM = √((1/4)²+(1/2)²) = √5/4.
AH = AN·AM/NM = (1/4)·(1/2)·4/√5 = √5/10 (высота из прямого угла).
Проведем прямую СS ⊥BL до пересечения с MN в точке S. пересечение этой прямой с прямой BL - точка Q. QS = НН1, так как AH1 перпендикулярна MN.
Продолжим C1Q и опустим на него перпендикуляр SR.
SR - искомое расстояние от прямой MN до плоскости ВС1L, так как С1Q ⊥ВL по теореме о трех перпендикулярах (CQ ⊥BL) и SQ ⊥BL по построению.
Продлим прямую BL до пересечения с прямой AD в точке D2. Треугольники ABD2 и DLD2 подобны (DL ||AB) c коэффициентом подобия k=AB/DL=2 => DL - средняя линия и BD2 = 2·BL = √5 (BL = √5/2 - найдено выше). AD2 = 2.
АН = √5/10 (найдено в первом пункте) .
Тогда высота из прямого угла треугольника ABD2 равна
АН1 = AB·AD2/BBD2 =2√5/5. =>
НН1 = АН1 - АН = 2√5/5 - √5/10 = 3√5/10.
SQ = HH1 = 3√5/10. (по построению).
СQ = BC·CL/BL = 1·(1/2)/(√5/2 ) = √5/5.
С1Q = √(СС1²+СQ²) = √(1+5/25) = √30/5.
Треугольники SQR и CQC1 подобны по острому углу с коэффициентом
k = SQ/C1Q = (3√5/10)/(√30/5) = √6/4.
SR = k·CC1 = k = √6/4 ≈ 0,61.
Расстояние между прямыми MN и С1L равно √6/4 ≈ 0,61.
Координатный метод:
Уравнение плоскости ВС1L:
Точки B(0;1;0), C1(1;1;1) и L(1;1/2;0)
|x-0 1 1 |
|y-1 0 -1/2 | = 0. => (1/2)·x - (y-1)·(-1) + (-1/2)·z = 0.
|z-0 1 0 |
Уравнение плоскости: (1/2)·x +y - (1/2)·z -1 = 0.
А = 1/2, В = 1, С = -1/2, D = -1.
По формуле расстояния от точки М(0;1.2;0) до плоскости:
d = |A·Mx + B·My + C·Mz + D|/√(A²+B²+C²). =>
d = |1/2·1/2 + 1·0 + (-1/2)·0 + (-1)|/√(1/4+1+1/4) = √6/4 ≈ 0,61.