Предмет: Алгебра,
автор: Татиана76
Помогите решить тригонометрическое неравенства 1/3sin3x>1/корень 12
Ответы
Автор ответа:
0
√12=2√3
(1/3)·sin3x > 1/√12;
·sin3x > 3/√12;
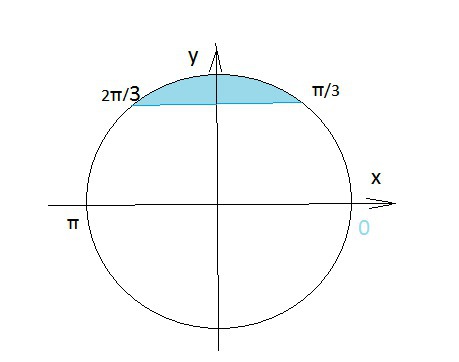
sin3x> √3/2
(π/3)+2πk < x < (2π/3) + 2πk, k ∈ Z.
Cм. решение на единичной окружности
и на графике
(1/3)·sin3x > 1/√12;
·sin3x > 3/√12;
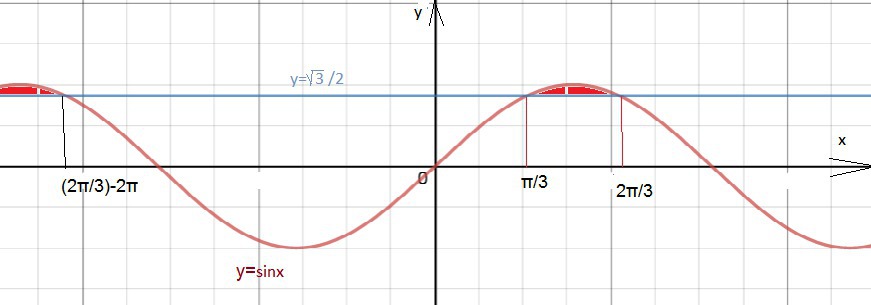
sin3x> √3/2
(π/3)+2πk < x < (2π/3) + 2πk, k ∈ Z.
Cм. решение на единичной окружности
и на графике
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: lola2378
Предмет: Алгебра,
автор: dayanchik756
Предмет: Математика,
автор: mikhailix
Предмет: Математика,
автор: Андрюшенька
Предмет: Литература,
автор: дианацу