Предмет: Геометрия,
автор: НютаСтолярова
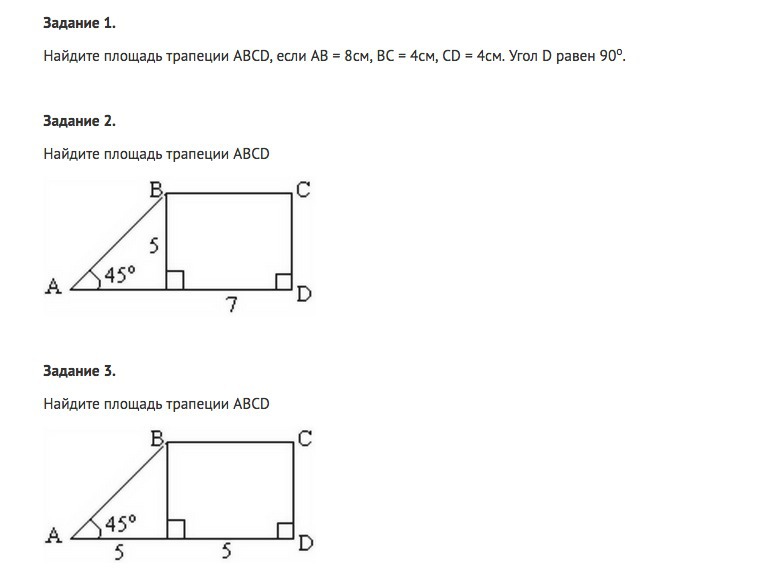
Помогите с геометрией умоляю
Приложения:
Ответы
Автор ответа:
0
№1
 прямоугольная трапеция (<D=90°)
прямоугольная трапеция (<D=90°)
 см
см
 см
см
 см
см
 ?
?

Из вершины B опустим перпендикуляр на сторону AD
 ⊥
⊥  и
и  , значит
, значит
 квадрат
квадрат
 см
см
Δ прямоугольный
прямоугольный
По теореме Пифагора найдем AK:
 см
см
 см
см
 cм²
cм²
№2
1 вариант: ( если AD=7 cм)
 прямоугольная трапеция (<D=90°)
прямоугольная трапеция (<D=90°)
 см
см
 см
см

 ?
?

Из вершины B опустим перпендикуляр на сторону AD
 ⊥
⊥ 
 прямоугольник
прямоугольник


Δ прямоугольный,
прямоугольный, 
 ⇒ Δ
⇒ Δ  равнобедренный и
равнобедренный и  см
см

 см
см
 см
см
 см²
см²
2 вариант: (если KD=7 см)
 прямоугольная трапеция (<D=90°)
прямоугольная трапеция (<D=90°)
 см
см
 см
см

 ?
?

Из вершины B опустим перпендикуляр на сторону AD
 ⊥
⊥ 
 прямоугольник
прямоугольник
 см
см
 см
см
Δ прямоугольный,
прямоугольный, 
 ⇒ Δ
⇒ Δ  равнобедренный и
равнобедренный и  см
см

 см
см
 см²
см²
№ 3
 прямоугольная трапеция (<D=90°)
прямоугольная трапеция (<D=90°)
 см
см
 см
см

 ?
?

Из вершины B опустим перпендикуляр на сторону AD
 ⊥
⊥ 
 прямоугольник
прямоугольник
 см
см

Δ прямоугольный,
прямоугольный, 
 ⇒ Δ
⇒ Δ  равнобедренный и
равнобедренный и  см
см

 см
см
 см²
см²
Из вершины B опустим перпендикуляр на сторону AD
Δ
По теореме Пифагора найдем AK:
№2
1 вариант: ( если AD=7 cм)
Из вершины B опустим перпендикуляр на сторону AD
Δ
2 вариант: (если KD=7 см)
Из вершины B опустим перпендикуляр на сторону AD
Δ
№ 3
Из вершины B опустим перпендикуляр на сторону AD
Δ
Автор ответа:
0
спасибо, а ко второй зд оба варианта писать?
Автор ответа:
0
на рисунке не очень понятно AD или KD равно 7 см - я рассмотрела два случая
Автор ответа:
0
а, спасибо большое!
Похожие вопросы
Предмет: Алгебра,
автор: natasi91
Предмет: Геометрия,
автор: Аноним
Предмет: Английский язык,
автор: Аноним
Предмет: Биология,
автор: tc241