Предмет: Математика,
автор: shumakong
Решите,пожалуйста...
Приложения:
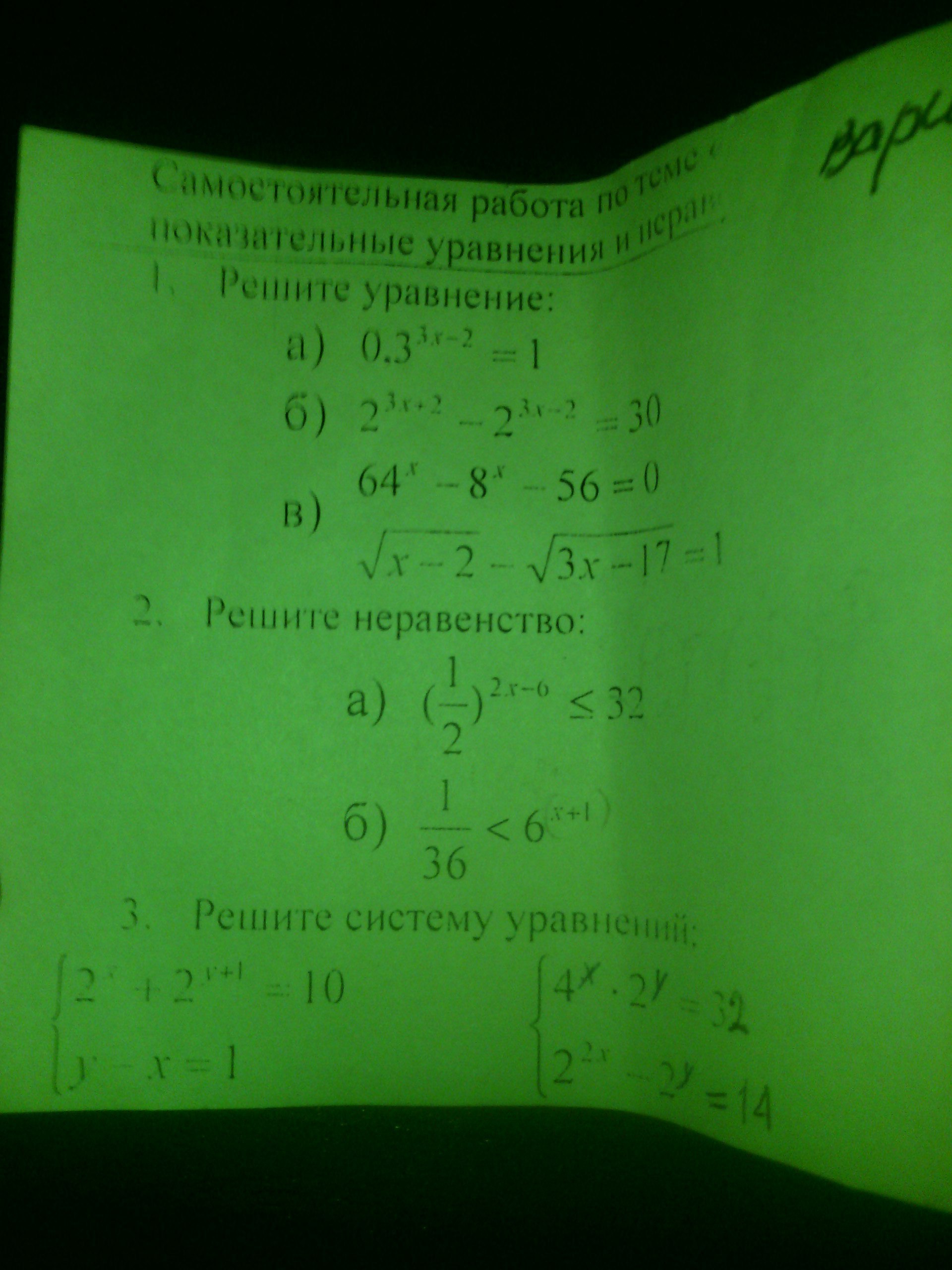
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: География,
автор: Аноним
Предмет: Литература,
автор: mollyyyyyyes
Предмет: Биология,
автор: albinalime2
Предмет: Математика,
автор: NastyaVasilev
Предмет: Литература,
автор: igor2134