Предмет: Алгебра,
автор: Аноним
g; помогите решить неравенство
Приложения:
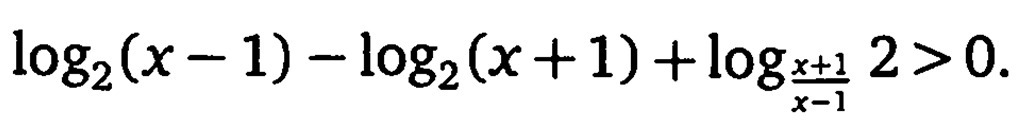
Ответы
Автор ответа:
0
ОДЗ
{x-1>0⇒x>0
{x+1>0⇒x>-1
{(x+1)/(x-1)>0⇒x<-1 U x>1
{(x+1)/(x-1)≠1⇒x+1≠x-1⇒x∈R
x∈(1;∞)
log(2)[(x-1)/(x+1)]+1/log[(x+1)/(x-1)]2>0
log(2)[(x-1)/(x+1)]-1/log(2)[(x-1)/(x+1)]>0
log(2)[(x-1)/(x+1)]=a
a-1/a>0
(a²-1)/a>0
(a-1)(a+1)/a>0
a=1 a=-1 a=0
_ + _ +
--------------(-1)-------------(0)-----------------(1)---------------
-1<a<0 U a>1
-1<log(2)[(x-1)/(x+1)]<0 U log(2)[(x-1)/(x+1)]>1
{log(2)[(x-1)/(x+1)]>-1⇒(x-1)/(x+1)>1/2⇒(2x-2-x-1)/(x+1)>0⇒(x-3)/(x+1)>0
{log(2)[(x-1)/(x+1)]<0⇒(x-1)/(x+1)<1⇒(x-1-x-1)/(x+1)<0⇒2/(x+1)>0
x<-1 U x>3 U x>-1⇒x>3
log(2)[(x-1)/(x+1)]>1
(x-1)/(x+1)>2
(x-1-2x-2)/(x+1)>0⇒(x+3)/(x+1)<0⇒-3<x<-1
Ответ x∈(3;∞)
{x-1>0⇒x>0
{x+1>0⇒x>-1
{(x+1)/(x-1)>0⇒x<-1 U x>1
{(x+1)/(x-1)≠1⇒x+1≠x-1⇒x∈R
x∈(1;∞)
log(2)[(x-1)/(x+1)]+1/log[(x+1)/(x-1)]2>0
log(2)[(x-1)/(x+1)]-1/log(2)[(x-1)/(x+1)]>0
log(2)[(x-1)/(x+1)]=a
a-1/a>0
(a²-1)/a>0
(a-1)(a+1)/a>0
a=1 a=-1 a=0
_ + _ +
--------------(-1)-------------(0)-----------------(1)---------------
-1<a<0 U a>1
-1<log(2)[(x-1)/(x+1)]<0 U log(2)[(x-1)/(x+1)]>1
{log(2)[(x-1)/(x+1)]>-1⇒(x-1)/(x+1)>1/2⇒(2x-2-x-1)/(x+1)>0⇒(x-3)/(x+1)>0
{log(2)[(x-1)/(x+1)]<0⇒(x-1)/(x+1)<1⇒(x-1-x-1)/(x+1)<0⇒2/(x+1)>0
x<-1 U x>3 U x>-1⇒x>3
log(2)[(x-1)/(x+1)]>1
(x-1)/(x+1)>2
(x-1-2x-2)/(x+1)>0⇒(x+3)/(x+1)<0⇒-3<x<-1
Ответ x∈(3;∞)
Автор ответа:
0
Ответ в приложениях (4 фотки)
Приложения:




Похожие вопросы
Предмет: Алгебра,
автор: VAse1398
Предмет: Алгебра,
автор: bugaevatanigmailcom
Предмет: Литература,
автор: kruush
Предмет: Литература,
автор: Наташаklass
Предмет: Математика,
автор: tmurzqgalirva