Предмет: Геометрия,
автор: zerodegrees
Найдите площадь равностороннего треугольника, сторона которого равна 12 см. (Напишите пожалуйста с объяснением)
Ответы
Автор ответа:
0
Ответ:
Sabc = 36√3 см²
Объяснение:
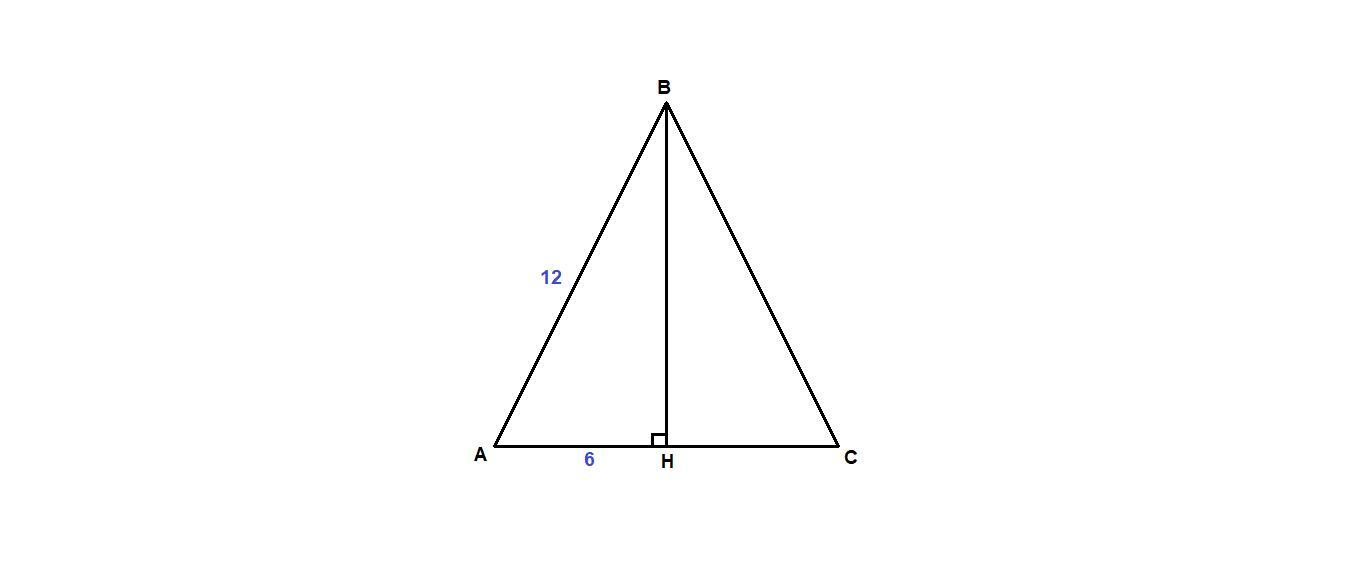
Проведем высоту ВН.
Высота в равностороннем треугольнике является медианой, поэтому
АН = НС = 1/2 АС = 1/2 · 12 = 6 см.
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
ВН² = АВ² - АН²
ВН² = 12² - 6² = 144 - 36 = 108
ВН = √108 = 6√3 см
Sabc = 1/2 AC · BH = 1/2 · 12 · 6√3 = 36√3 см²
Приложения:
Автор ответа:
0
Решение:
Проведем высоту BH
Тогда:
AH= HC = 1/2 AC = 1/2 × 12 = 6 см
Про треугольник ABH можем сказать, что:
/_ AHB = 90 градусов
BH^2=AB^2-AH^2=12^2-6^2=108
BH= _/(это обозначение корня) 108 = 6_/3 см
Следовательно,
Sabc=1/2 AC × BH = 6 × 6 _/3 =36 _/3 см2
Ответ: 36 _/3 см2
P.S. Если, что кнопки зависли, поэтому не могу поставить корень
Приложения:

Похожие вопросы
Предмет: География,
автор: rimp2006
Предмет: Математика,
автор: shirobokovkosta
Предмет: Математика,
автор: hlunstun
Предмет: Информатика,
автор: kurmetuatay