Предмет: Алгебра,
автор: kleo50
упростите выражение с решением
Приложения:
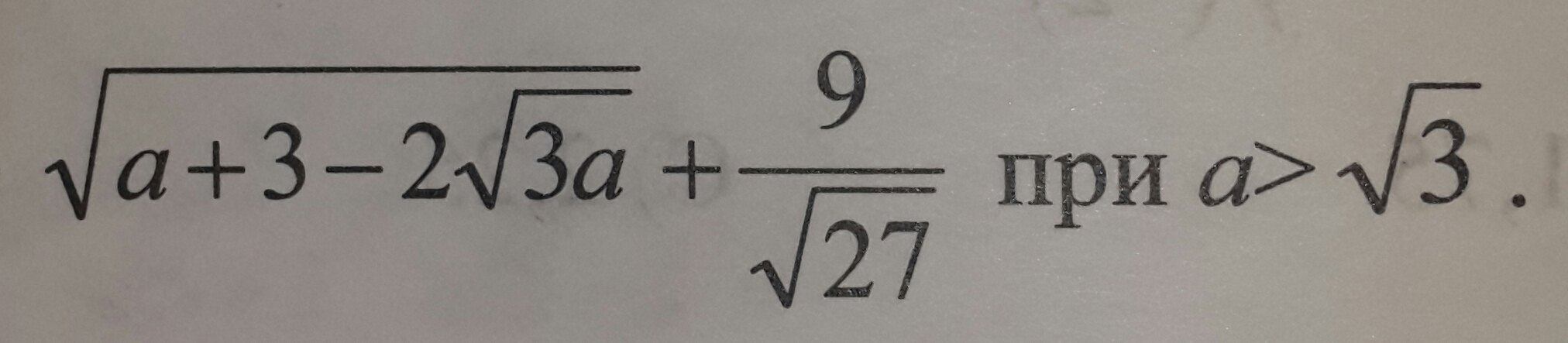
Ответы
Автор ответа:
0
Решение:
Подкоренное выражение является полным квадратом
Поэтому можно записать
Все решение выглядит правильным, если бы не одно,но
В условии а>√3 но это еще не значит что √а>√3
например 4>√3 (16>3), но √4<√3
но для того чтобы |√a-√3|=√a-√3 необходимо чтобы а>3
Поэтому решение предпологает два ответа:
- для а∈(√3;3) выражение равно 2√3-√а;
- для а∈[3;+∞) выражение равно √а.
Похожие вопросы
Предмет: Другие предметы,
автор: igemberdykyzym
Предмет: Алгебра,
автор: lclvovigprrr
Предмет: Окружающий мир,
автор: koncikovrasul
Предмет: Математика,
автор: ilinarosa
Предмет: Математика,
автор: rinatqaripov1