Предмет: Геометрия,
автор: Марина20000003
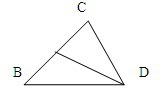
В треугольнике BCD стороны BD и CD равны, DM - медиана, угол BCD равен 38. Найдите углы BMD и BDM.
Приложения:
Ответы
Автор ответа:
0
Δ BCD-равнобедренный,следовательно,медиана в нем является высотой и биссектрисой.
BМD=90°т.к DМ-высота
BDМ=19°т.к DМ-биссектриса и делит угол ВDC пополам 38/2=19
BМD=90°т.к DМ-высота
BDМ=19°т.к DМ-биссектриса и делит угол ВDC пополам 38/2=19
Автор ответа:
0
Сначала доказываешь что треугольник BDC равнобедренный, это значит что из вершины медиана равна высоте и биссиктрисе.
известно что биссиктриса делит угол по полам, в данном случае угол BDC, 38:2=19. Т. К. DM еще и высота, то значит что BMD = 90 градусов.
известно что биссиктриса делит угол по полам, в данном случае угол BDC, 38:2=19. Т. К. DM еще и высота, то значит что BMD = 90 градусов.
Похожие вопросы
Предмет: Математика,
автор: nikcom65
Предмет: Английский язык,
автор: ma1980go1229erali
Предмет: Обществознание,
автор: madalievruslan12
Предмет: Химия,
автор: 1983gulya