Предмет: Алгебра,
автор: reisunya
1) F(x)=x^5+2x^3+3x-11
[-1;1]
2) F(x)=2x+3* корень из x^2 в степени 3
[-8;1]
Найти максимум и минимум функции
Приложения:
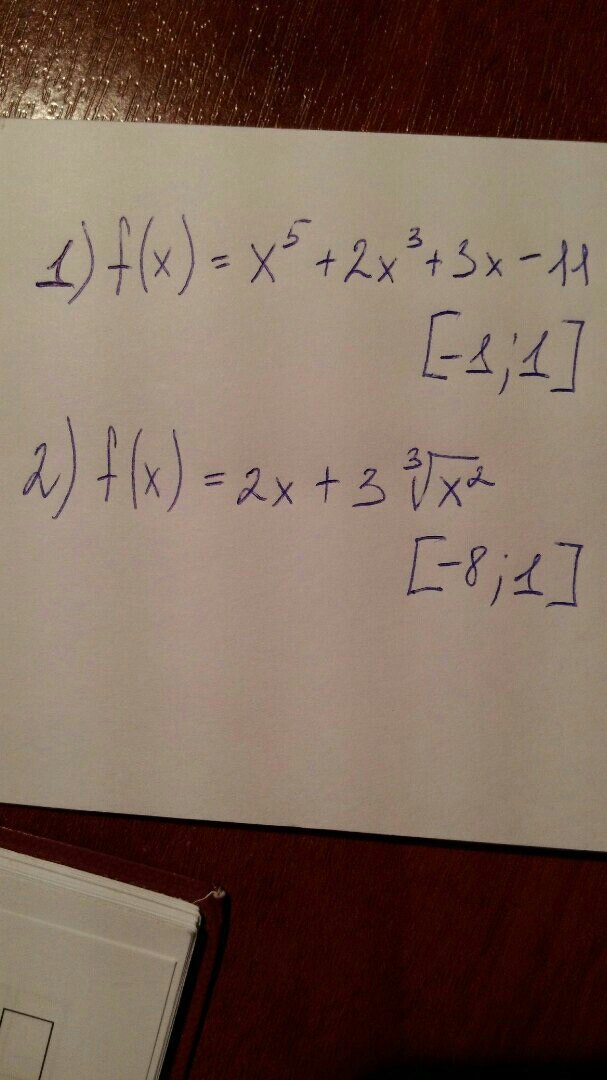
Ответы
Автор ответа:
0
1)
F(x)=x⁵+2x³+3x-11
F'(x)=5x⁴+6x²+3
5x⁴+6x²+3=0
Пусть t=x²
5t²+6t+3=0
f(t)=5t²+6t+3 - парабола, ветви которой направлены вверх.
D=6² - 4*5*3=36-60= -24<0
Парабола не пересекает ось ОХ.
Парабола лежит выше оси ОХ.
Функция f(t)=5t²+6t+3 имеет только положительные значения, а значит, F'(x)=5x⁴+6x²+3 тоже имеет только положительные значения. То есть производная больше нуля, и исходная функция только возрастает - нет экстремумов.
На промежутке [-1; 1]:
F(-1)=(-1)⁵+2*(-1)³+3*(-1)-11=-1-2-3-11=-17 - минимальное значение
F(1)=1⁵+2*1³+3*1-11=1+2+3-11= -5 - максимальное значение.
2)
F(x)=2x+3*³√x²
F'(x)=2+3*(²/₃)*x^(- ¹/₃)=2 + 2/x³
2+2/x³ =0
ОДЗ: x≠0
2/x³ = -2
x³= -1
x= -1 - экстремум функции
-1∈[-8; 1]
На промежутке [-8; 1]:
F(-8)=2*(-8) + 3 * ³√(-8)² = -16 + 3*4= -4 - минимальное значение
F(-1)=2*(-1) + 3 * ∛(-1)² = -2 + 3=1
F(1)=2*1 + 3 * ∛1² = 2+3=5 - максимальное значение
F(x)=x⁵+2x³+3x-11
F'(x)=5x⁴+6x²+3
5x⁴+6x²+3=0
Пусть t=x²
5t²+6t+3=0
f(t)=5t²+6t+3 - парабола, ветви которой направлены вверх.
D=6² - 4*5*3=36-60= -24<0
Парабола не пересекает ось ОХ.
Парабола лежит выше оси ОХ.
Функция f(t)=5t²+6t+3 имеет только положительные значения, а значит, F'(x)=5x⁴+6x²+3 тоже имеет только положительные значения. То есть производная больше нуля, и исходная функция только возрастает - нет экстремумов.
На промежутке [-1; 1]:
F(-1)=(-1)⁵+2*(-1)³+3*(-1)-11=-1-2-3-11=-17 - минимальное значение
F(1)=1⁵+2*1³+3*1-11=1+2+3-11= -5 - максимальное значение.
2)
F(x)=2x+3*³√x²
F'(x)=2+3*(²/₃)*x^(- ¹/₃)=2 + 2/x³
2+2/x³ =0
ОДЗ: x≠0
2/x³ = -2
x³= -1
x= -1 - экстремум функции
-1∈[-8; 1]
На промежутке [-8; 1]:
F(-8)=2*(-8) + 3 * ³√(-8)² = -16 + 3*4= -4 - минимальное значение
F(-1)=2*(-1) + 3 * ∛(-1)² = -2 + 3=1
F(1)=2*1 + 3 * ∛1² = 2+3=5 - максимальное значение
Похожие вопросы
Предмет: Информатика,
автор: elenashulmina2103
Предмет: Биология,
автор: sergejovcharenko2011
Предмет: Математика,
автор: anzelikabilokur
Предмет: Математика,
автор: ira3015