Предмет: Алгебра,
автор: olyaevzhenko
Объясните, пожалуйста. Почему 0-0+0/1-0. Тема: "предел последовательности"
Приложения:
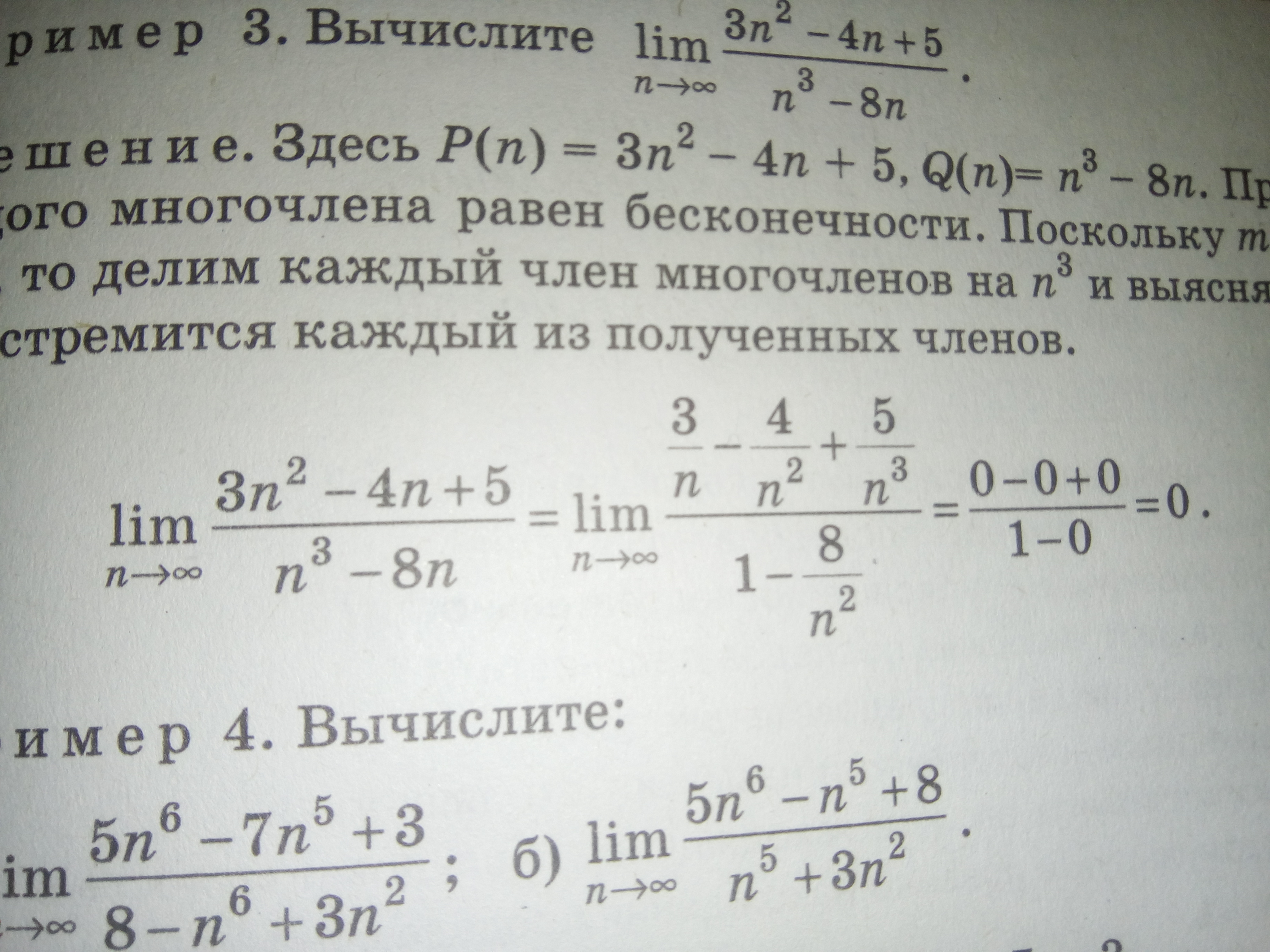
Ответы
Автор ответа:
0
любое число деленное на бесконечно большую величину(∞) будет бесконечно мало т.е стремиться к 0
Автор ответа:
0
чтобы вычислить предел, нужно вместо n подставить значение к которому оно стремится. В данном случае - это бесконечность.
Еще нужно помнить (если речь идет о пределах) что любое число (C), кроме нуля, при делении на бесконечность (бесконечно большую величину), дает нуль(бесконечно малую величину)

Таким образом полный разбор примера будет таким:
1) Сначала подставим в исходный предел значение n равное бесконечности

Получилась неопределенность (то что в фигурных скобках)
Чтобы ее раскрыть, делим каждое слагаемое и числителя и знаменателя на старшую степень...
В нашем случае старшая степень - это n³, идем дальше

Еще нужно помнить (если речь идет о пределах) что любое число (C), кроме нуля, при делении на бесконечность (бесконечно большую величину), дает нуль(бесконечно малую величину)
Таким образом полный разбор примера будет таким:
1) Сначала подставим в исходный предел значение n равное бесконечности
Получилась неопределенность (то что в фигурных скобках)
Чтобы ее раскрыть, делим каждое слагаемое и числителя и знаменателя на старшую степень...
В нашем случае старшая степень - это n³, идем дальше
Похожие вопросы
Предмет: Математика,
автор: nikitakfli24
Предмет: Українська мова,
автор: xiomimi3xx
Предмет: Математика,
автор: eliseyshmelev08
Предмет: Математика,
автор: Kemmerd