Предмет: Алгебра,
автор: Nastradamsik
решите уравнение x^4+x^2-2=0 ,заменив x^2=y
Ответы
Автор ответа:
0
Биквадратное уравнение решается заменой переменной.

x₂ = -2 не является корнем уравнения, т.к. квадрат любого числа имеет положительный знак.
x₂ = -2 не является корнем уравнения, т.к. квадрат любого числа имеет положительный знак.
Автор ответа:
0
Также обратной теоремой Виета можно была запросто найти корни уравнения.
Автор ответа:
0
Вот,...................
Приложения:
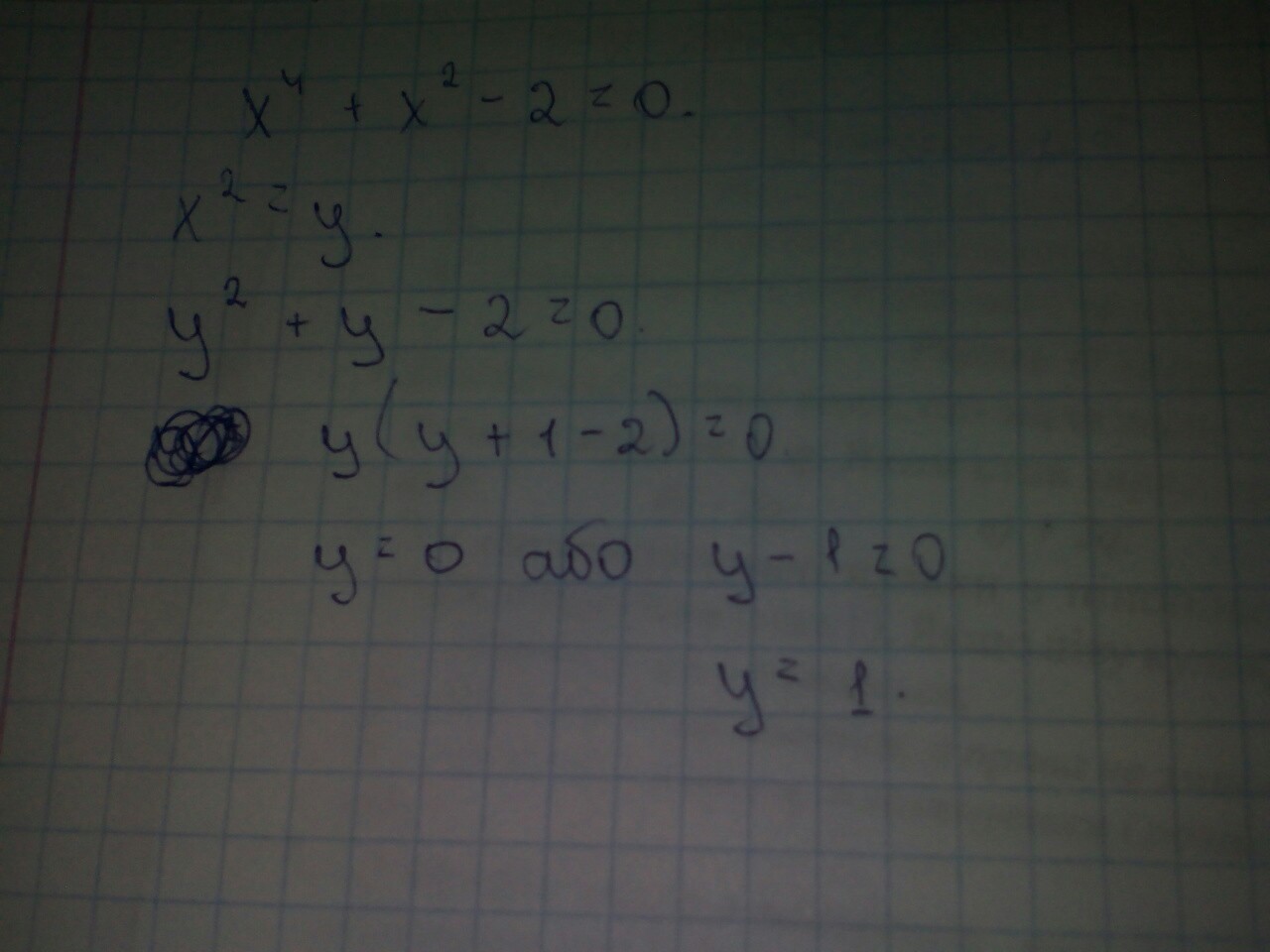
Похожие вопросы
Предмет: Математика,
автор: lavanator2006
Предмет: Математика,
автор: gradinarmarina463
Предмет: Химия,
автор: Аноним
Предмет: География,
автор: svetahov1204