Предмет: Алгебра,
автор: Raskolnikov1
Помогите пожалуйста решить! Даю 60 баллов
Приложения:
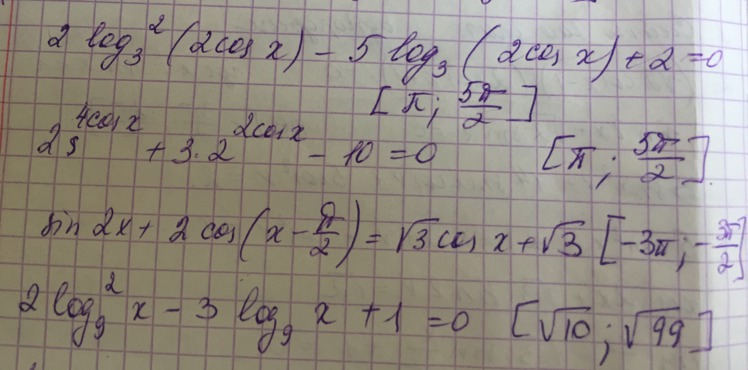
Ответы
Автор ответа:
0
1) 





![[ pi ;5 pi 2]
x=2 pi + pi /6=13 pi /6
x=2 pi - pi /6=11 pi /6 [ pi ;5 pi 2]
x=2 pi + pi /6=13 pi /6
x=2 pi - pi /6=11 pi /6](https://tex.z-dn.net/?f=%5B+pi+%3B5+pi+2%5D%0A%0Ax%3D2+pi+%2B+pi+%2F6%3D13+pi+%2F6%0A%0Ax%3D2+pi+-+pi+%2F6%3D11+pi+%2F6)
*********************
2)



![[ pi ;5 pi /2]
x=2 pi - pi /3=5 pi /3
x=2 pi + pi /3=7 pi /3 [ pi ;5 pi /2]
x=2 pi - pi /3=5 pi /3
x=2 pi + pi /3=7 pi /3](https://tex.z-dn.net/?f=%5B+pi+%3B5+pi+%2F2%5D%0A%0Ax%3D2+pi+-+pi+%2F3%3D5+pi+%2F3%0A%0Ax%3D2+pi+%2B+pi+%2F3%3D7+pi+%2F3)
*************************
3)


![[-3 pi ;-3 pi /2]
x=-3 pi
x=-2 pi + pi /3=-5 pi /3 [-3 pi ;-3 pi /2]
x=-3 pi
x=-2 pi + pi /3=-5 pi /3](https://tex.z-dn.net/?f=%5B-3+pi+%3B-3+pi+%2F2%5D%0A%0Ax%3D-3+pi+%0A%0Ax%3D-2+pi+%2B+pi+%2F3%3D-5+pi+%2F3)
*****************
4)




![[ sqrt{10}; sqrt{99}]
x=9 [ sqrt{10}; sqrt{99}]
x=9](https://tex.z-dn.net/?f=%5B+sqrt%7B10%7D%3B+sqrt%7B99%7D%5D%0A%0Ax%3D9++)
*********************
2)
*************************
3)
*****************
4)
Похожие вопросы
Предмет: Математика,
автор: itachi056
Предмет: Английский язык,
автор: csgokovalyov
Предмет: Английский язык,
автор: mariamamonova740
Предмет: География,
автор: kudaibergenov75