В прямоугольном треугольнике АВС (<С=90 градусов) АВ=10 см, радиус вписанной в него окружности равен 2 см. Найти площадь этого треугольника.
Я знаю, что площадь надо найти по формуле S=1/2*P*r
Периметр начала находить по свойству касательных, и учитель сказал, что это правильно, и сказал дорешать, но у меня проблемы с уравнением. Начала находить по теореме Пифагора, но тут возникли проблемы с ответом: он получался либо больше, либо получалось отрицательное число. Помогите! Заранее огромное спасибо)
Ответы
Я так понимаю, нам необходимо найти только периметр?
Ниже рисунок.
Отрезки а и b в сумме дают 10 см, так как из таких же а и б состоит и гипотенуза.
И тогда периметр треугольника равен 10+10+4=24 (см)
А 4 - отрезки от радиуса, это понятно, да?)
Тогда S=24*2/2=24 см²
Ответ: 24 см²
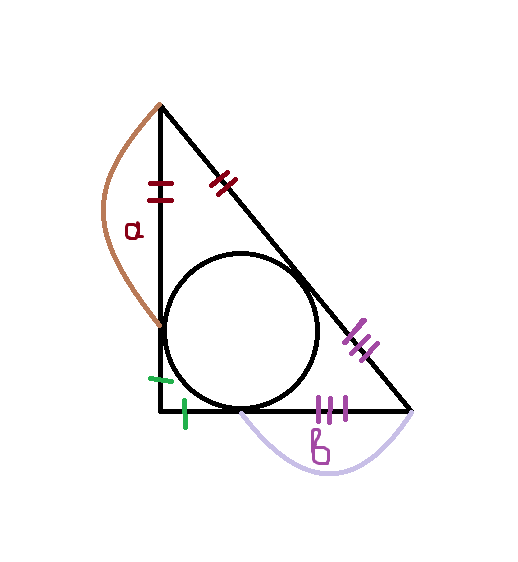
Треугольник АВС, С=90, М - точка касания на АВ, Н -точка касания на ВС., К-точка касания на АС. проводим радиусы ОК = ОН перпендикулярно точкам касания. КОНС - квадрат, КС=НС=ОН=ОК=2, АК=АМ - как касательные из одной точки = а, ВМ=ВН=10-а как касательные
ВС= ВН+НС =10-а+2 = 12-а, АС=АК+КС=а+2
АВ в квадрате = АС в квадрате + ВС в квадрате
100= (а+2) в квадрате + (12-а) в квадрате
2а в квадрате - 22а +48 = 0
а = (22+-корень(484 - 4 х 2 х 48 )) / 4
а1= 4
а2=8 - не подходит кает не равен гипотенузе
АС = 4 + 2 = 6
ВС = 12 - 4 = 8
площадь = 1/2 АС х ВС = 1/2 х 6 х 8 = 24
