Предмет: Алгебра,
автор: kreep19
Помогите пожалуйста выполнить
Приложения:
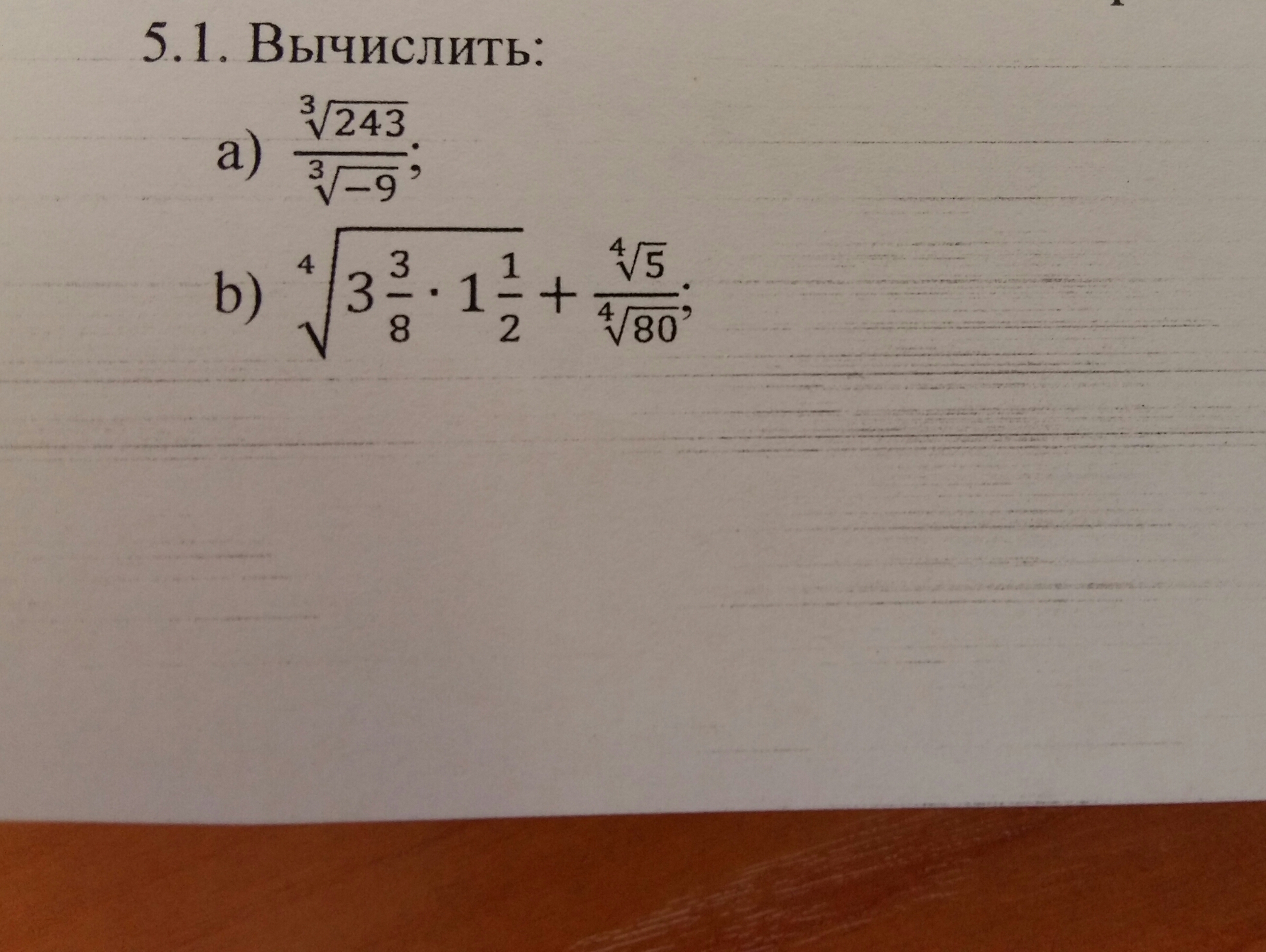
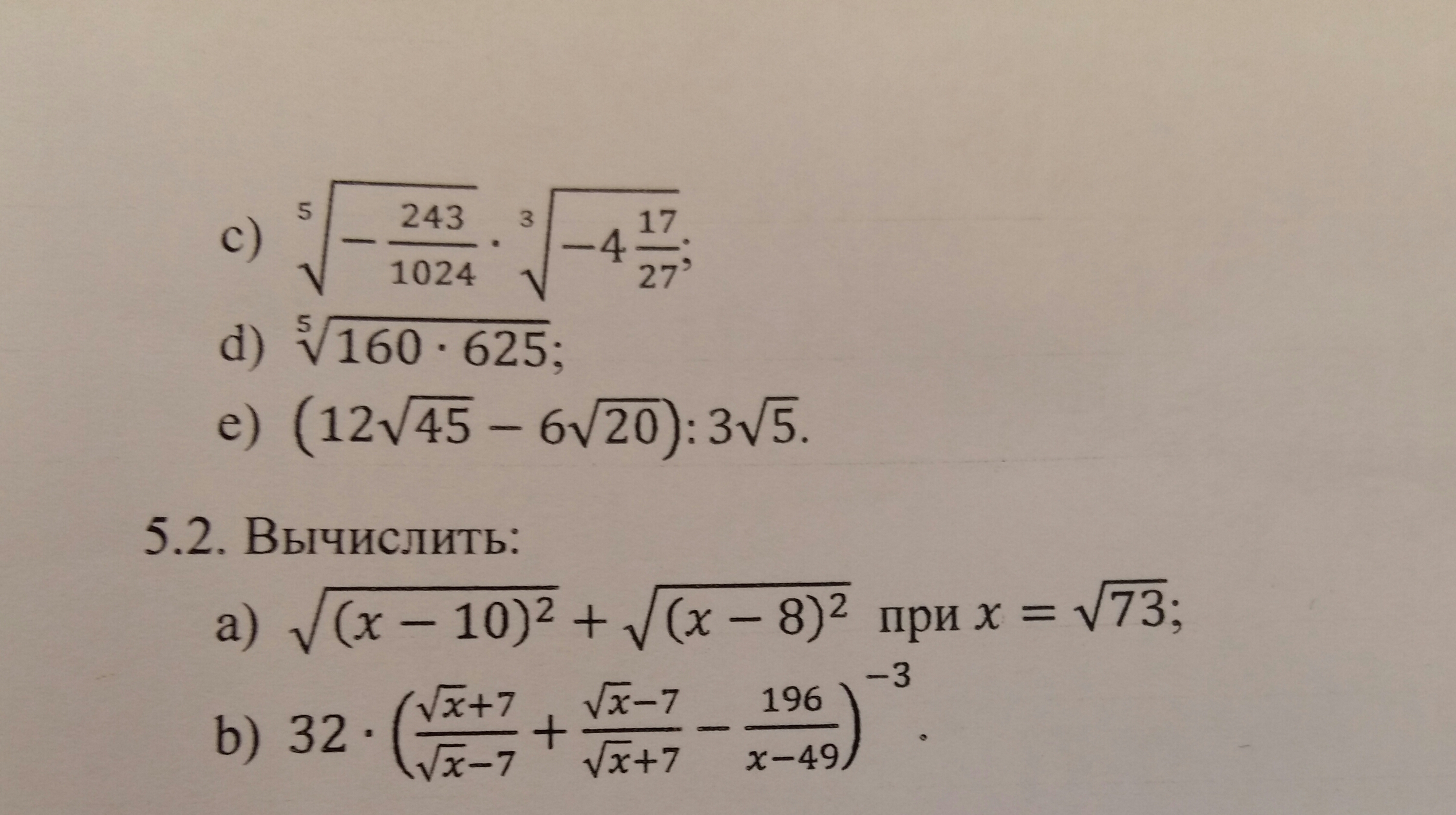
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Литература,
автор: 2127321273
Предмет: Физика,
автор: lulinanasta4
Предмет: Математика,
автор: YALA420
Предмет: Литература,
автор: 175831
Предмет: Физика,
автор: kristinamohito