Предмет: Математика,
автор: MIlM
√3cos2 x=sinxcosx
cos2 x+sinxcosx=0
объясните,как такое решать)
Ответы
Автор ответа:
0
Применены табличные значения тригонометрических функций
Приложения:
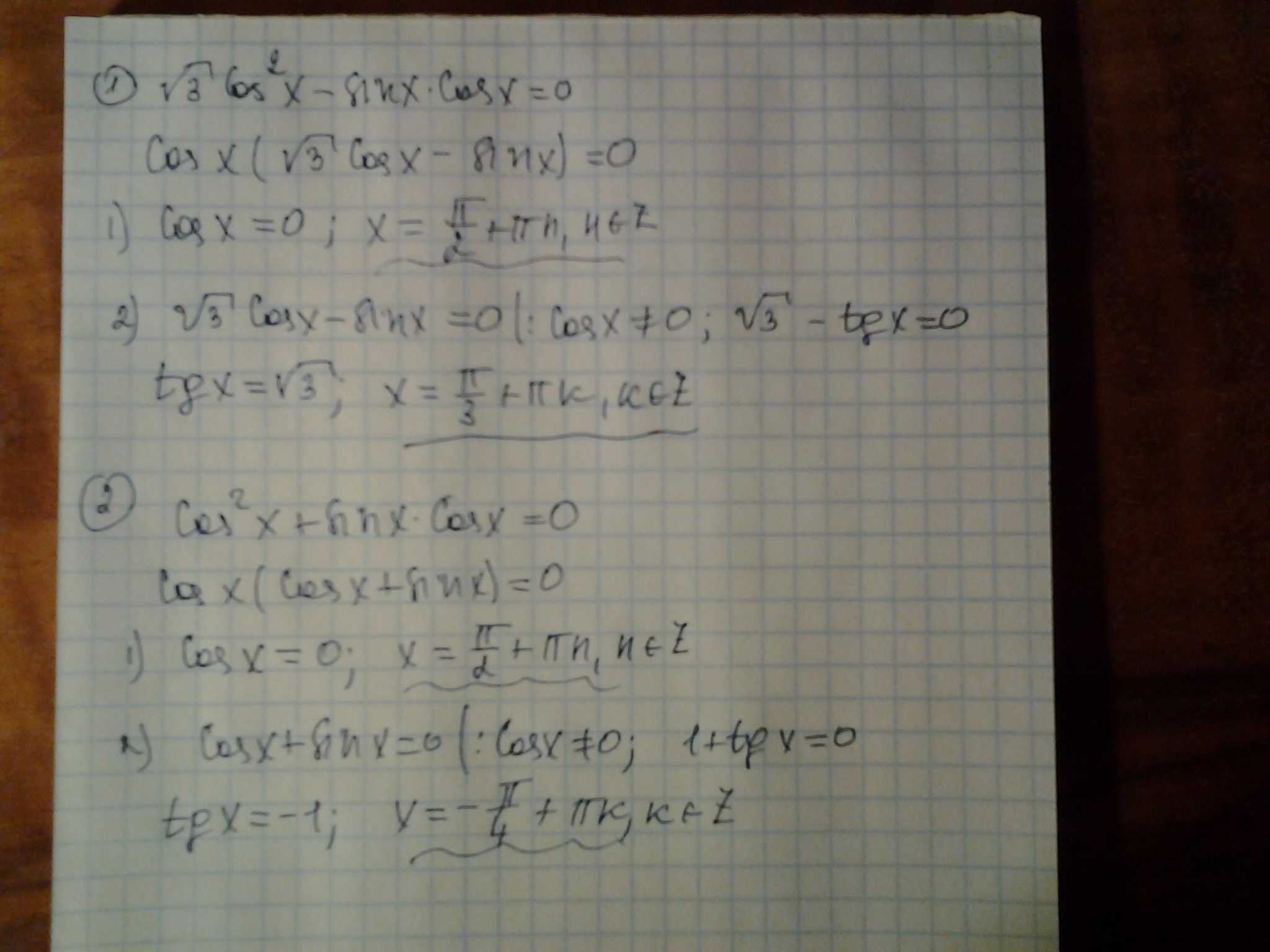
Автор ответа:
0
1)√3cos2 x=sinxcosx
Решение
2√3cos2 x=2sinxcosx
2√3cos2 x=sin2x
tg2x=2√3
2x=arctg 2√3+πn, где€N
x= 1/2arctg 2√3+(πn)/2
2) cos2 x+sinxcosx=0
Решение
cos2 x=-sinxcosx
2cos2 x=-2sinxcosx
2cos2 x=-sin2x
tg2x=-2
2x=-arctg 2+πn, где€N
x= -1/2arctg 2+(πn)/2
Решение
2√3cos2 x=2sinxcosx
2√3cos2 x=sin2x
tg2x=2√3
2x=arctg 2√3+πn, где€N
x= 1/2arctg 2√3+(πn)/2
2) cos2 x+sinxcosx=0
Решение
cos2 x=-sinxcosx
2cos2 x=-2sinxcosx
2cos2 x=-sin2x
tg2x=-2
2x=-arctg 2+πn, где€N
x= -1/2arctg 2+(πn)/2
Похожие вопросы
Предмет: Українська література,
автор: taniacumak2009
Предмет: Русский язык,
автор: kimadel1
Предмет: Математика,
автор: fiuesvhouefho
Предмет: Математика,
автор: AnutiK15
Предмет: Литература,
автор: jroslov