Предмет: Математика,
автор: SergeyShein
Помогите пожалуйста исследовать функции на экстремум!!!
Приложения:
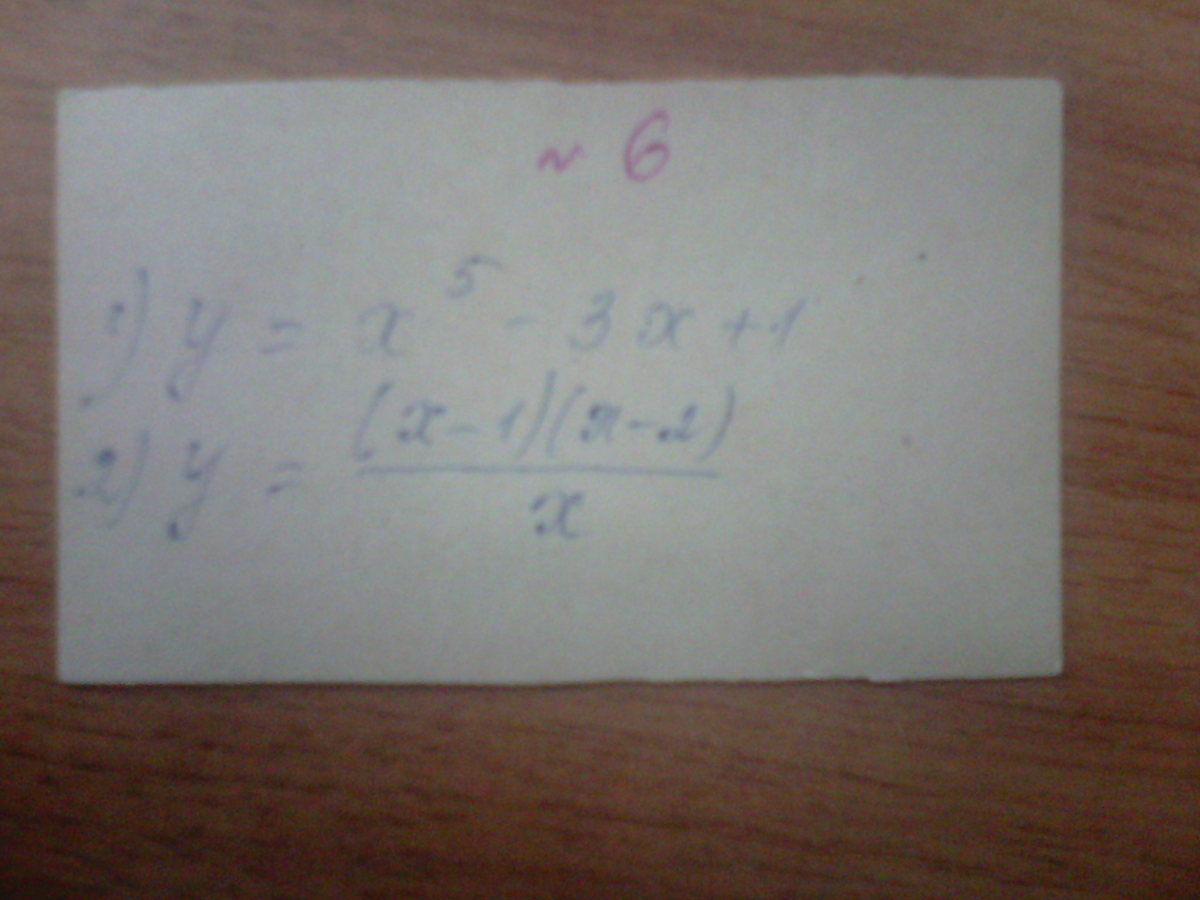
Ответы
Автор ответа:
0
1.
на интервале производная положительна, а значит функция возрастает.... между корнями производная отрицательна и значит функция убывает... следовательно первый корень - локальный экстремум (максимум) а второй - локальный экстремум(минимум)
график в первом вложении
2.
между корнями производная отрицательна - функция убывает
вне корней производная положительна - функция возрастает
следовательно первый корень - локальный экстремум (максимум)
второй корень - локальный экстремум(минимум)
кроме того функция имеет две асимптоты
x=0
y = x-3
график во втором вложении
Похожие вопросы
Предмет: Русский язык,
автор: binyatova03
Предмет: Другие предметы,
автор: MaratelloMaJo2012
Предмет: Информатика,
автор: Аноним
Предмет: Математика,
автор: Eva3813
Предмет: Литература,
автор: Аноним