Question

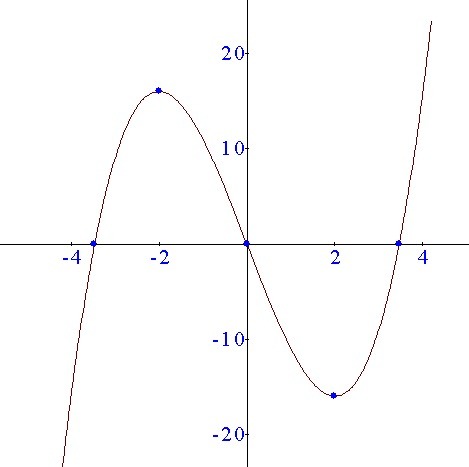
y=x^3-12x полное исследование функции) помогите плиз!

Answer 1

1. Область определения функции: множество всех действительных чисел.

2. Не периодическая функция.

3. Проверим на четность или нечетность функции:

$y(-x)=(-x)^3-12cdot(-x)=-x^3+12x=-(x^3-12x)=-y(x)$

Итак, функция является нечетной.

4. Точки пересечения с осью Ох и Оу:

4.1. С осью Ох (у=0):

$x^3-12x=0\ x(x^2-12)=0\ x_1=0;~~ x_{2,3}=pmsqrt{12}$

4.2. С осью Оу (x=0):

$x=0;~ y=0^3-12cdot 0=0$

5. Критические точки, экстремумы, возрастание и убывание функции.

$y'=(x^3-12x)'=(x^3)'-(12x)'=3x^2-12\ y'=0;~~~ x^2-4=0\ x=pm 2$

___+____(-2)___-__(2)_____+____

Функция возрастает на промежутке x∈(-∞;-2) и x∈(2;+∞), а убывает - x ∈ (-2;2). Производная функции в точке х=-2 меняет знак с (+) на (-), следовательно точка х=-2 - локальный максимум, а в точке х=2 производная функции меняет знак с (-) на (+), значит точка х=2 - локальный минимум.

6. Точки перегиба.

$y''=(3x^2-12)'=6x\ y''=0\ x=0$

На промежутке x ∈ (-∞;0) функция выпукла вверх, а на промежутке x ∈ (0;+∞) выпукла вниз.

7. Горизонтальной, вертикальной и наклонной асимптот нет.