Предмет: Математика,
автор: JuliaHelp
3 биквадратных уравнения
Приложения:
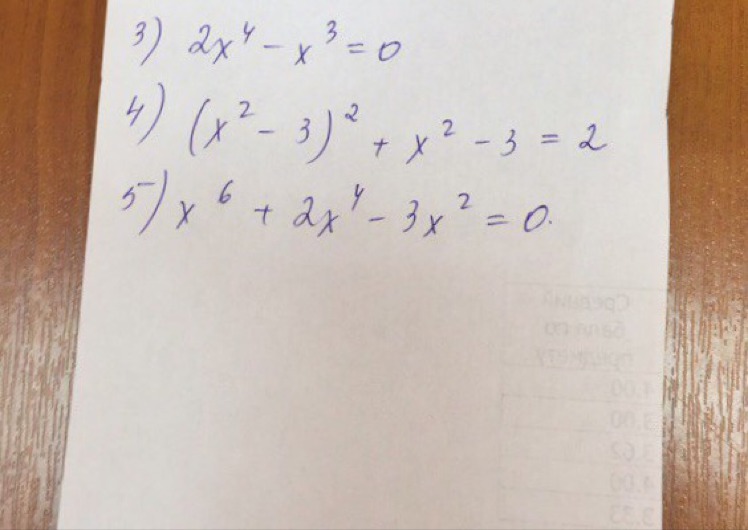
Ответы
Автор ответа:
0
Ответ: 0,12
Пусть
Теперь вернемся в замену и найдем х, причем уравнений будет два
Ответ: +-2 и +-1
5.
Пусть у=
Теперь вернемся в замену и найдем х, причем уравнений будет два
Ответ: +-1
Похожие вопросы
Предмет: Математика,
автор: allalife
Предмет: Русский язык,
автор: Dghfrfgguutcgh
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: dexnex
Предмет: Химия,
автор: vano2511