Предмет: Алгебра,
автор: ГОСТЬ2014
Помогите решить 164 номер
Приложения:
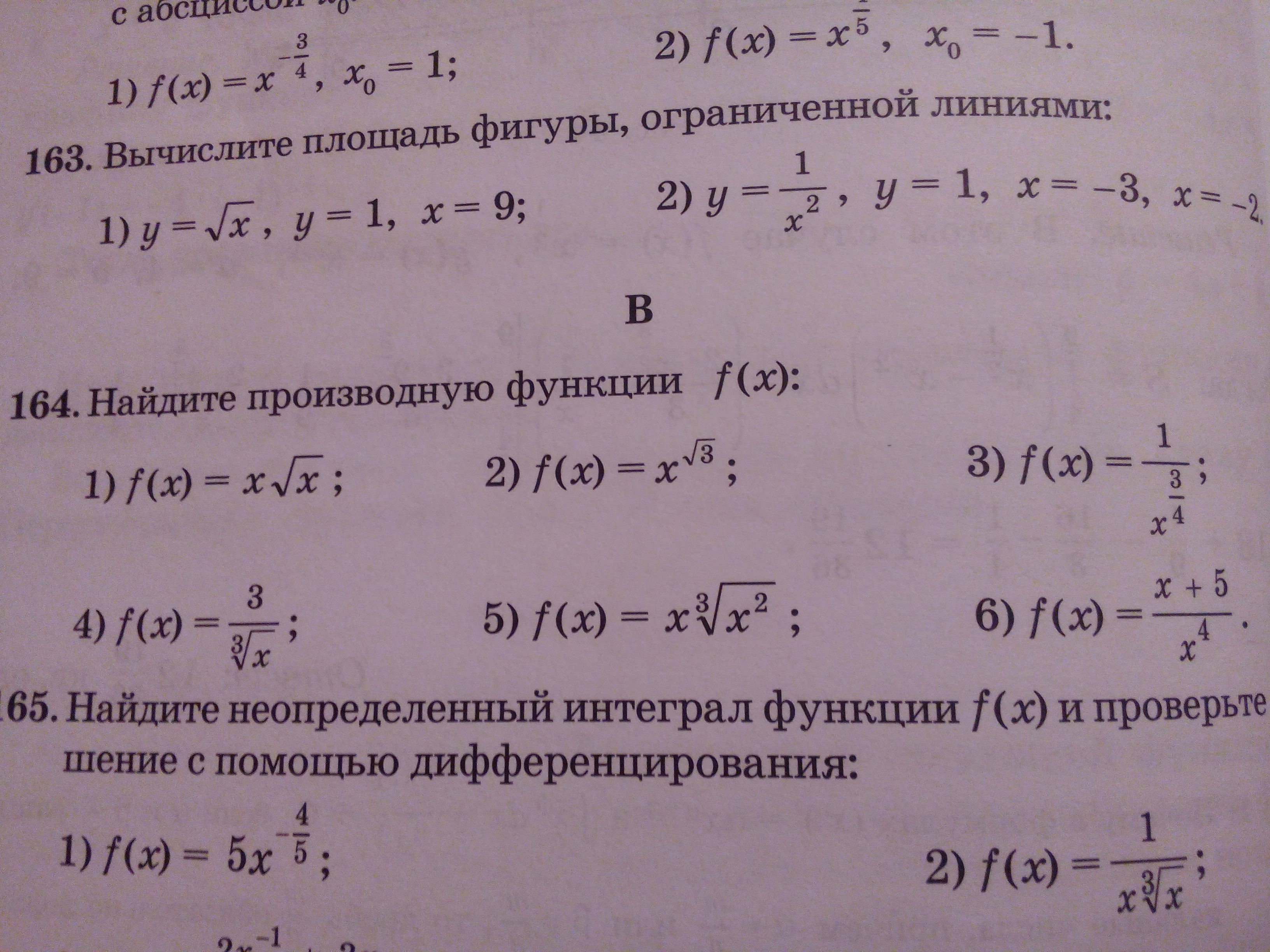
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: География,
автор: vasiliy1167
Предмет: Литература,
автор: saroinika2008
Предмет: Литература,
автор: seldomborisov
Предмет: Обществознание,
автор: soiferolga
Предмет: Биология,
автор: katerina08082004