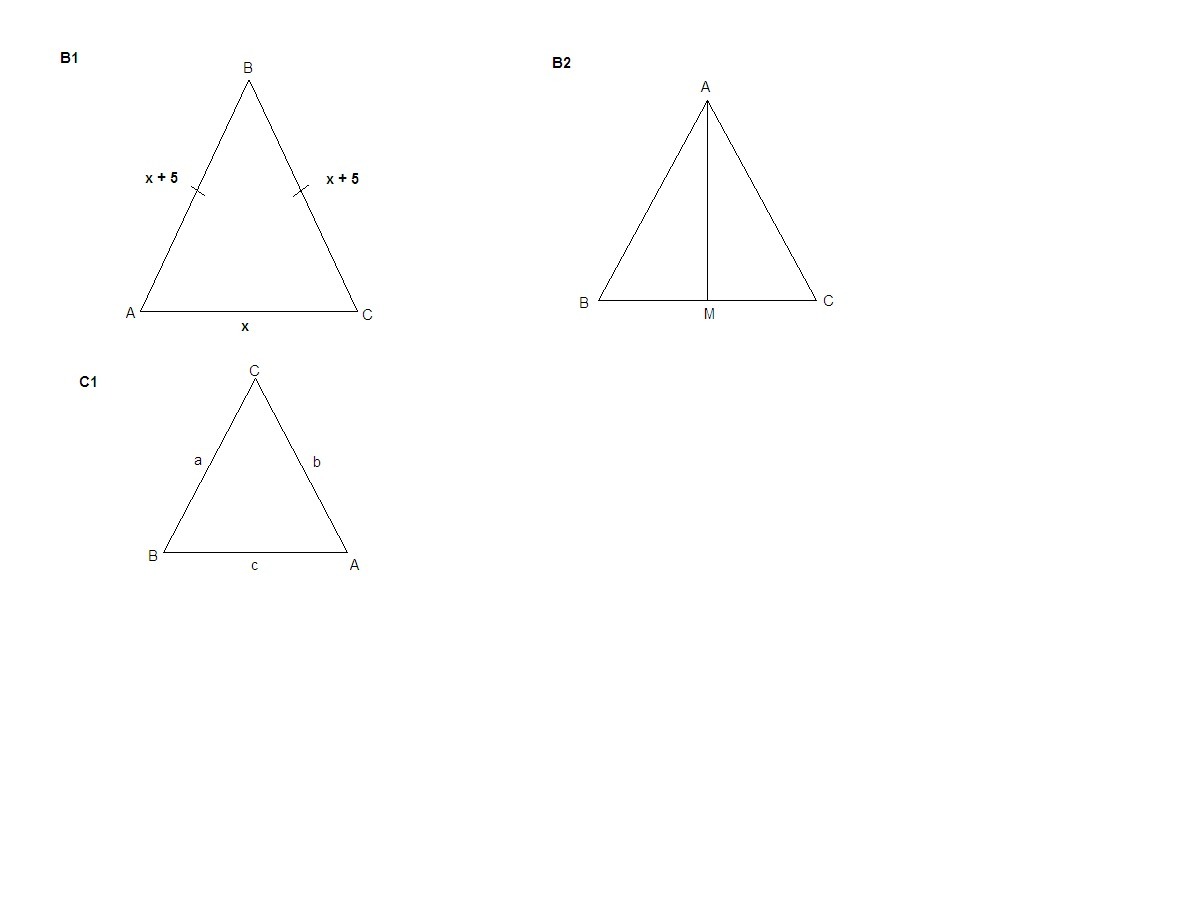
Помогите решить
А1. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
1) может быть неверно 3) всегда неверно
2) может быть верно 4) всегда верно
А2. Если треугольник равнобедренный, то:
1) все его стороны равны
2) любая его медиана является биссектрисой и высотой
3) все его углы равны
4) одна из его высот совпадает с биссектрисой и медианой
A3. Периметр равнобедренного треугольника равен 48 см, боковая сторона — 15 см. Чему равно основание этого тре¬угольника?
1)16,5 см 3)18см
2) 16см 4)24см
А4. В треугольнике АВС высота ВК делит сторону АС по полам, градусная мера угла А равна 68°. Чему равна вели¬чина угла С?
1) 68° 3)22°
2)32° 4)44°
В1. Периметр равнобедренного треугольника равен 34 см. Основание меньше боковой стороны на 5 см. Найдите бо¬ковую сторону.
В2. В равнобедренном треугольнике ЛВС с основанием ВС проведена медиана AM. Периметр ∆ АВС равен 40 см, а периметр ∆АВМ— 33 см. Найдите длину медианы AM.
С1. Сумма двух сторон равнобедренного треугольника равна 26 см, а периметр равен 36 см. Какими могут быть стороны этого треугольника?
Ответы
А1. Ответ: 4.
А2. Ответ: 4.
А3. Ответ: 3.
А4. Ответ: 1.
В1. Дано: ΔАВС, АВ = ВС = АС + 5 см, Р = 34 см.
Найти: АВ.
Решение: Пусть АС = х см, тогда АВ = ВС = х + 5,
x + (x + 5) + (x + 5) = 34
3x + 10 = 34
3x = 24
x = 8
АС = 8 см
АВ = ВС = 8 + 5 = 13 см
Ответ: боковая сторона 13 см.
В2. Дано: ΔАВС, АВ = АС, АМ - медиана, Pabc = 40 см, Pabm = 33 см.
Найти: АМ.
Решение:
Pabm = 33 см
АВ + ВМ + АМ = 33
2 · (АВ + ВМ + АМ) = 66
Так как АВ = АС, а ВМ = СМ, то
2АВ + 2ВМ + 2АМ = 66
АВ + АС + ВС + 2АМ = 66
2АМ = 66 - (АВ + АС + ВС) = 66 - Pabc = 66 - 40 = 16
AM = 16/2= 8 см
С1. 1) Если сумма равных сторон равна 26 см, то боковые стороны равны по 13 см, а основание - 10 см.
2) Обозначим боковые стороны а и b, основание - с.
а + с = 26 см
Рabc = 2а + с = 36 см
с = 36 - 2а
с = 26 - а
26 - a = 36 - 2a
a = 10 см
c = 16 см
Ответ: 13 см, 13 см, 10 см или 10 см, 10 см, 16 см.